ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 1. Теоретический материал
 

1. Последовательности, заданные рекуррентным соотношением.

Если каждый последующий член числовой последовательности выражается функциональным образом через предыдущие и при этом определены первые k ее членов, то говорят, что последовательность {a_n} задана рекуррентно. Само число k можно назвать степенью, либо глубиной рекуррентности.

Простейшими примерами таких последовательностей являются арифметическая и геометрическая прогрессии: — геометрическая. Что касается арифметической прогрессии, то ее можно задать разными способами:

а) , б) .

Однако, рекуррентное соотношение не обязательно должно являться линейным. Так, для вычисления квадратного корня из положительного числа A, строят последовательность приближений по формуле 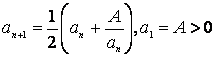. По подобной формуле можно строить последовательность приближенных значений корня любой степени k, заменив в знаменателе дроби в скобке величину an на ее k-1-ю степень.

Для решения многих практических задач, особенно финансового содержания, большое значение имеют линейные рекуррентные соотношения, которые еще называют дискретными, или разностными уравнениями. Их общий вид

Если член g(n) тождественно равен нулю, то уравнение однородное — содержит только «a» k –е, притом в первой степени, в противном случае — неоднородное. Как правило, g(n) есть полином от текущего номера n, но может быть и n-м членом геометрической прогрессии.

II. Решение однородных линейных уравнений

Рассмотрим на примере однородных уравнений степени рекуррентности k=2, или порядка 2:

.

Для любого однородного уравнения справедливы следующие свойства.

1) Если решение (его еще называют частным решением), то

— тоже решение.

2) Если и — решения, то и их сумма/разность тоже является решением.

Из этих свойств следует, что любая линейная комбинация частных решений с произвольными коэффициентами тоже решение такого уравнения. А множество всех без исключения частных решений называют общим решением дискретного уравнения.

Частное решение обычно ищут в виде . Подставив в уравнение, получим .

После умножения обеих частей уравнения на получим характеристическое, или вековое уравнение — .

Если оно имеет различные действительные корни , то общим решением будет . Это означает, что каково бы ни было частное решение , найдутся единственные , такие, что .

Если же корни кратные , то — легко показать, общим решением будет .

Так, в частности, для уравнения , задающего арифметическую прогрессию, характеристическое уравнение имеет кратный корень . Соответственно, общее решение имеет вид , и оно задает множество всех прогрессий, в т. ч. с нулевой разностью. Начальные условия однозначно определят постоянные в линейной комбинации

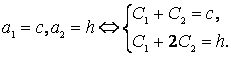
Если характеристическое уравнение имеет корень λ кратности m=3, 4 и т. д., то в общем решении наряду с другими будет слагаемое , где первый множитель есть многочлен степени не выше m-1. (Все зависит от начальных условий).

В том случае, когда характеристическое уравнение имеет комплексные корни, применяется матричный подход, при котором рассматриваются векторы, координаты которых суть m подряд идущих членов последовательности. Последняя как бы «нарезается» на куски длиной m.

Однако, для k=2 можно просто использовать комплексные числа. При этом сами рекуррентные последовательности и соответствующие им линейные дискретные уравнения могут альтернативно использоваться для введения собственно комплексных чисел как воображаемых корней векового уравнения. (Традиционно их вводят для решения трехчленных кубических уравнений без вывода рабочей формулы, см. комплект Г.К Муравина для профильного обучения.)

III. Неоднородные уравнения: свойства решений

Если и — суть решения некоторого неоднородного уравнения, то их линейная комбинация — тоже является решением.

Сама такая комбинация носит название симплектической.

1) Если к некоторому частному решению неоднородного линейного уравнения добавить произвольное решение соответствующего однородного, то мы вновь получим другое частное решение. Это позволяет найти общее решение неоднородного уравнения путем сложения некоторого его частного решения с общим решением однородного.

2) И наоборот, разность двух частных решений неоднородного уравнения есть решение соответствующего однородного.

3) Если и — суть частные решения неоднородных уравнений с одними и теми же однородными членами, но с разными неоднородными частями g₁(n) и g₂(n), то их сумма y_n =f(n)+g(n) есть частное решение аналогичного уравнения с неоднородной частью g₃(n) =g₁(n) +g₂(n). Это позволяет отыскивать частное решение по частям («принцип разламывания веника»), а потом части складывать.

4) A z_n=Cf(n)— частное решение уравнения с неоднородным членом Сg₁(n).

Наиболее важные случаи решений рассмотрены в Приложении 2 на уравнениях 1-го порядка, играющих очень важную роль в финансовой математике и не только. Основная идея — путем замены переменной свести уравнение к простейшему однородному, решение которого — геометрическая прогрессия.

*) Уравнения вида .

Нетрудно видеть, что при p =1, b ≠0 в качестве решения мы получим n-й член арифметической прогрессии, а при b =0, p ≠1 — общий член геометрической прогрессии. Обе они, как говорят математики, являются гомотопиями общего решения данного уравнения.

Если p≠1,то решение имеет вид 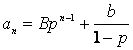. В противном случае — .

**) Уравнения вида .

Уравнение сводят к однородному заменой . Тогда

.

Для однородности необходимо “ликвидировать” свободный член. Это возможно, если

.

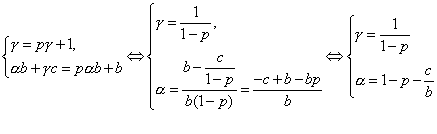
Тогда решением будет

В случае p=1 решение — .

В общем случае, если неоднородная часть есть P_m (n) —полином степени m от номера n, а p=1 решение есть .

***) Уравнения вида .

Если p≠q, то решение ищут в виде .

Тождество выполняется для произвольных p и q, если

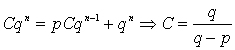. Тогда .

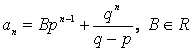Обычно это записывают как .

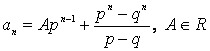Особый случай p = q — резонанс, и решение имеет вид .

Стоит обратить внимание, что уравнения 1-го порядка содержат всего одну произвольную постоянную, значение которой однозначно находится из каких-то не переопределенных условий.

Содержание

вернуться на страницу Дистанционная поддержка