Материалы к уроку

Тайны равнобедренного треугольника
(тексты заданий)

 

Исследование 1:

Черепашка нарисовала горизонтальный отрезок АВ. Вернулась в точку А и смотрит в направлении на восток (рис. 1). Достройте этот отрезок до треугольника так, чтобы углы при основании АВ были равны (рис. 2).

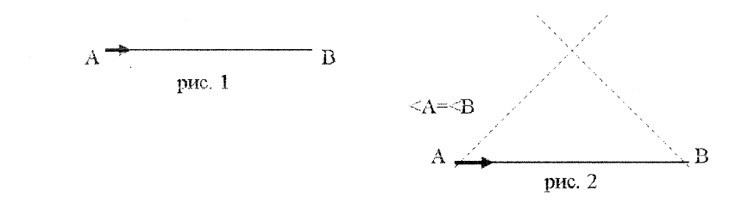
Задание 1: Исследуйте длины получившихся сторон.

Задание 2: Постройте еще несколько треугольников с другими величинами углов при основании АВ. Сделайте вывод о полученных треугольниках. (Ввести понятия равнобедренного треугольника, боковых сторон)

Задание 3: Постройте несколько треугольников с одинаковой величиной углов при основании, но с разными длинами основания. Сделайте вывод о полученных треугольниках

Задание 4: Попробуйте построить треугольники с одинаковыми углами при основании, величины которых либо равны 90 градусам, либо больше 90 градусов. Сделайте вывод об этих треугольниках.

Задание5: Используя результат задания 4, попробуйте сформулировать условие необходимое для углов при основании, чтобы треугольник можно было построить.

Исследование 2:

Черепашка построила горизонтальный отрезок АВ, в середине этого отрезка развернулась на 90⁰ в левую сторону и, нарисовав другой отрезок CD, повернулась в направлении на юг (рис4).

 

Задание 1: Из любой точки отрезка CD постройте линии, у которых <ACD и <BCD равны. (рис. 5)

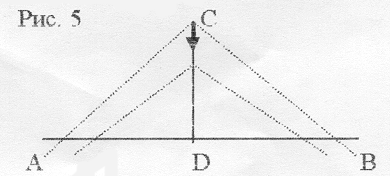
Задание 2: Исследуйте длины получившихся боковых сторон треугольников. Сделайте вывод о получившихся треугольниках.

Задание 3: Измерьте расстояния от вершин каждого из получившихся треугольников до отрезка CD. Сделайте вывод о длинах этих отрезков. (Ввести понятие биссектрисы равнобедренного треугольника)

Исследование 3:

Постройте равнобедренный треугольник (см. исследование 1). Переместите Черепашку на середину основания (рис. 3).

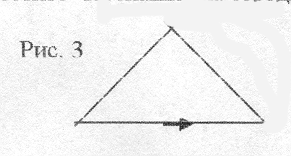
На какой угол должна повернуться Черепашка, чтобы при движении вперед прийти в противоположную вершину?

Задание 1: Постройте линию из середины основания. Сделайте вывод о построенной линии.

Задание 2: Выполните такое же построение из середин боковых сторон равнобедренного треугольника. Сравните полученные результаты с результатами задания 1, сделайте вывод о свойстве линии, проведенной из середины основания равнобедренного треугольника под углом 90⁰. (Ввести понятие медианы и высоты равнобедренного треугольника).

Занятие 4: Подготовка статей к выпуску газеты на тему “Мои открытия в равнобедренном треугольнике”.

Черепашка строит треугольник с одинаковыми углами при основании.

Примечание: Курсивом выделен материал для учителя, на который следует обратить внимание.

В начале занятия следует обсудить с детьми, какой треугольник мы строили до сих пор, например, когда рисовали с помощью Черепашки крышу дома. Тогда это был треугольник с одинаковыми сторонами и углами.

Напомним, что равносторонний треугольник строился как замкнутый многоугольник с помощью следующей программы:

ПОВТОРИ 3 [ВПЕРЕД 50 ВПРАВО 360 / 3]

При этом Черепашка поворачивалась на угол в 360 / 3=120 градусов, а мы ранее обсуждали с детьми, что поворот производится на дополнительный угол, который также называется внешним, так что собственно угол треугольника равен 180 - 120 = 60 градусов

Тот факт, что сумма смежных углов равна 180 градусам, вытекает из предыдущих рассуждений: для того, чтобы построить развернутый угол, Черепашке надо повернуться на полоборота в любую сторону, а полоборота и есть 180 градусов, как мы выясняли в самом начале работы с Черепашкой при введении градусной меры угла. (см.., например, [1], [4]).

Итак, мы рисовали крышу в виде треугольника, у которого, по нашему построению, были все стороны равны и все углы по 60 градусов.

Вопрос к детям: Каким будет такой треугольник?

Такой треугольник будет называться правильным, так как в нем равны между собой все стороны и все углы.
Значит, если у треугольника хотя бы один угол не равен 60 градусам, то такой треугольник не является правильным. Теперь посмотрим, будут ли у него равны стороны.
Для дальнейших исследований свойств треугольника договоримся с детьми о терминологии. Так как, например, крыша дома лежит на коробке дома, т.е. у треугольника в этом случае есть нижняя сторона. Назовем такую сторону треугольника основанием, тогда две другие стороны - боковыми.
Вообще, отвлекаясь от крыши и от дома, будем рассматривать треугольники, "лежащие" на горизонтальной стороне.

Вопрос: Пусть у нас есть треугольник АВС, назовите основание.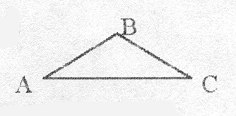
В данном случае основанием будет сторона АС. А С

Вопрос: Какие стороны у нашего треугольника являются боковыми?
Стороны АВ и ВС.

Далее следует провести небольшую беседу (длительностью 3 – 5 минут) о том, как человечество приобретает новые знания. Можно попросить детей привести примеры открытий, сыгравших, по их мнению, важную роль, а также назвать имена ученых, совершивших эти открытия. При этом обсудить, что на первых порах использовался метод “проб и ошибок”, т.е. пробовались разные варианты решения возникшей задачи, анализировались результаты и делался какой-то вывод. (Так мы делали в курсе Роботландии при работе с "Черными ящиками", и именно этим методом мы воспользуемся на нашем уроке.) После этого сказать детям, что сейчас у них есть возможность выступить в роли таких ученых при исследовании свойств треугольника.

Предложение поиграть в ученых, которые будут заниматься исследованиями и в результате сделают математическое открытие, вызовет интерес.

Цель игры - построить треугольник, у которого одинаковые углы при основании, но не равные 60 градусам, т.к. свойства правильного треугольника мы уже знаем. Затем будем измерять боковые стороны шагами Черепашки, поскольку наша цель - проверить: чему равны стороны треугольника, у которого равны углы при основании.

Этапы построения.

Сначала строим отрезок - основание треугольника. Выберем его произвольной длины, например, 50 шагов черепашки. Вы знаете, что в исходном положении черепашка стоит в центре и смотрит на север.

Вопрос: Чтобы начертить горизонтальный отрезок справа налево, что она должна сделать? Нужно повернуть влево на 90 градусов и пройти 50 шагов. В командах это будет: ЛВ 90 ВП 50.

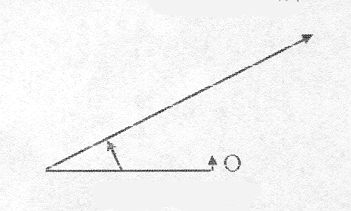
ЛВ 30 ВП 100

Повернем Черепашку лицом к середине отрезка:

Вопрос: Какие команды нужно дать нашей Черепашке, чтобы отложить угол, например, 30 градусов и провести линию в 100 шагов  (длину стороны мы не знаем и берем примерно)?
Чтобы построить последнюю сторону следует вернуться в точку О. Это место начального положения черепашки и центр экрана.

Вопрос: Как проще вернуться в точку О, не рисуя переход?
ПП ДОМОЙ ПО
Здесь черепашку повернем тоже лицом к середине отрезка, отложим такой же угол -30 градусов, но уже вправо, и проведем прямую линию длиной в 100 шагов.

Вопрос: Назовите команды, которые должна выполнить Черепашка?
ЛВ 90 ПР 30 ВП 100
Как видно из рисунка, боковые стороны пересеклись в точке. Обозначим ее В.

Вопрос: Какую фигуру мы получили в результате нашего построения?
Треугольник.

Вопрос: Какие углы при основании этого треугольника?
Равные.
Измерим теперь боковые стороны треугольника, который мы построили. Подумаем, как это можно сделать.

Учащиеся могут предлагать различные способы измерения сторон, самый простой из них - сначала вернуться в точку, откуда мы только что пришли, т. к. нам известно, какова длина пройденного пути. Таким образом, мы подводим их к первой команде:

НД 100

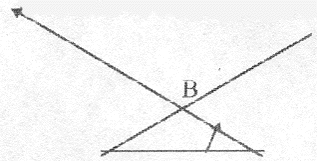
Теперь будем последовательно мелкими шагами двигаться к точке В и при этом складывать шаги.

Как только дойдем до точки В, полученный результат следует тут же записать в тетрадь. Для более наглядного и точного измерения можно сменить цвет черепашки и спрятать ее (это, например, НЦ 5 СЧ)
Команда ДОМОЙ установит черепашку в исходную точку и повернет ее на север. Повторив самые первые построения, двигаясь вдоль другой боковой стороны до точки В, подсчитаем длину другой стороны.
Оба результата нужно сообщить, чтобы записать их на доске или кодоскопе.
Детям предлагается устроить соревнование, где у всех равные шансы первыми сделать построение. Для этого целесообразно разбить участников на группы, не более 2 человек в группе, и проделать за машиной все этапы построения. Все команды следует писать в командной строке. Естественно, при измерении длин сторон могут возникнуть небольшие расхождения и здесь необходимо сказать, что эти длины примерно равны. При больших расхождениях в результатах измерений, нужно проверить правильность построения треугольника (например, длину основания, равные ли при нем углы).

Каждая группа ученых сначала будет строить треугольники с заданнми углами при основании (для этого целесообразно распределить, кто какие углы будет использовать при построении: 20°, 40°,50°, 70°, 75°, 80° и др.), а затем любые,по желанию.

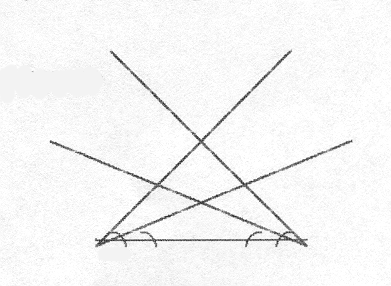
Результаты исследований будут фиксироваться на доске в виде таблицы.

Группа ученых	Баллы	Длины боковых сторон		Углы при основании
		1	2
1. Ира и Лена				30
2. Катя и Сережа				40
…				…

“Ученые” начинают работу за машинами. По мере поступления результатов таблица заполняется. Если есть незначительные расхождения в длинах сторон, попросить измерить еще раз. Если расхождения значительные, проверить правильность построения и измерения сторон. В графе "баллы" можно по усмотрению учителя присуждать баллы: за правильное и быстрое построение (до 5 баллов), за точные измерения( 3 балла), за активную работу при разборе этапов построения(3 балла), за большее количество исследований(3 балла), а так же за оригинальные выводы при анализе заполненной таблицы( до 5 баллов). По результатам измерений, выписанных в таблицу, предложить детям сделать выводы.

Тем из учащихся, которые закончили работу раньше других, дается задание построить треугольник с углами при основании 0є и 90є. Эту особую ситуацию следует обсудить после формулировки выводов по остальным результатам эксперимента.

Группа ученых	Баллы	Длины боковых сторон.		Углы при основании
		1	2
1. Ира и Лена		29	29	30
2. Катя и Сережа		32	32	40
…	…	…	…	…
…	…	95	95	75

 

В ходе дискуссии учащиеся формулируют различным образом те выводы, к которыми они пришли в результате собственных исследований. Итогом такой дискуссии должен явиться некоторый вывод, рожденный сообща всеми учащимися. Этот вывод записывается учителем на доске для всеобщего обозрения, после чего учащиеся заносят его в тетради. Ниже приводится пример такого вывода.

Вывод 1: если в треугольнике углы при основании равны, то и боковые стороны равны.

Такой треугольник является равнобедренным.

Вывод 2: чем больше углы при основании в равнобедренном треугольнике, тем больше боковые стороны.

Дети, построившие треугольники с углами при основании 0 или 90 градусов, делятся своими исследованиями и демонстрируют свои построения. С углами в 0 градусов боковые стороны оказались лежащими на основании, треугольник не получился и вообще от него осталась одна линия, а при построении треугольника с углами 90 градусов боковые стороны не пересеклись и поэтому треугольник не получился. Можно задержаться на последнем случае и порассуждать о том, что есть прямые, которые не пересекаются.

Для поощрения творческой исследовательской активности детей в дальнейшем, целесообразно оценить их работу как очень нужную и важную и аттестовать высокой отметкой.