Материалы к уроку

Черепашка вычисляет число ПИ

Примечание: На предыдущем занятии дети получают задание написать небольшой реферат, посвященный жизни и исследованиям Архимеда.

Сегодня на уроке мы вместе с Черепашкой попробуем совершить одно из открытий великого ученого древности Архимеда.
Мы знаем, что благодаря этому человеку и созданным им небывалым военным машинам город Сиракузы был неприступен при взятии его римлянами. Знаменитым восклицанием “Эврика” (что в переводе означает “нашел”) мы тоже обязаны Архимеду. Можно сказать, что Архимед был великим математиком древности, но в равной степени он был и военным инженером, и астрономом, и физиком.
Итак, Черепашка поможет нам сегодня стать “Архимедами”. Для наших исследований потребуются процедуры для рисования окружностей разных размеров.

Первое исследование: Пусть Черепашка нарисовала ОКРУЖНОСТЬ1 (окружность первого размера) и остановилась в точке А . Как Черепашке оказаться в противоположной точке B?

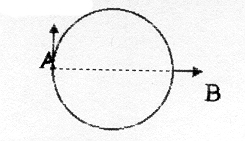
Для этого можно предложить различные варианты. Например, пройти половину окружности и повернуться влево на 90⁰.

Вопрос 1: Нет ли другого способа? Конечно есть. Пройти по прямой “сквозь” окружность.

Вопрос 2:Какие команда должна выполнить Черепашка в этом случае? Повернуться вправо на 90⁰ и сделать сколько-то шагов.

Вопрос 3: Но как определить нужное количество шагов?
Пусть Черепашка продвигается на небольшое количество шагов, пока не попадет в противоположную точку. А затем мы сосчитаем это количество шагов.
Итак, в результате первого исследования мы получили, что Черепашка прошла путь длиной 114 шагов.

Вопрос 4: Не знает ли кто-нибудь, как называется путь, проделанный Черепашкой? Это диаметр. Значит, окружность первого размера имеет диаметр длиной 114 шагов.

Второе исследование: Измерьте диаметр окружности второго, третьего и четвертого размера.

Результат наших исследований:

ОКРУЖНОСТЬ1 - диаметр 114 шагов;
ОКРУЖНОСТЬ2 - диаметр 57 шагов;
ОКРУЖНОСТЬ3 - диаметр 38 шагов;
ОКРУЖНОСТЬ4 - диаметр 28.5 шагов.

Третье исследование: Теперь надо получить значения для длин окружностей.

Вопрос 5: Как вы понимаете, что такое длина окружности? Каким образом мы можем ее измерить? Длина окружности - это длина того пути, который проделывает Черепашка при рисовании окружности (длина, конечно, измеряется шагами Черепашки).

Вопрос 6: Сколько шагов длина ОКРУЖНОСТИ1? Вспомним, какие команды выполняет Черепашка при рисовании окружности:

ПОВТОРИ 360 [ВП 1 ПР 1]. Т.е. она 360 раз шагает на 1 шаг и попадает в исходную точку. Окружность замкнулась, и в итоге Черепашка сделала 360 шагов. Значит, длина ОКРУЖНОСТИ1 - 360 шагов.

Вопрос 7: Какова длина окружностей второго, третьего и четвертого размера?

Итак, в результате третьего исследования мы получили:

длина ОКРУЖНОСТИ1 - 360 шагов;
длина ОКРУЖНОСТИ2 - 180 шагов;
длина ОКРУЖНОСТИ3 - 120 шагов;
длина ОКРУЖНОСТИ4 - 90 шагов и т.д.

Теперь остался самый важный этап на пути к званию “Архимед - 97”. В связи с этим уместно вспомнить, как вообще делаются многие великие открытия. Великий ученый что-нибудь измеряет, или вычисляет какие-нибудь числа. И вдруг ему приходит в голову мысль:”А что если из первого числа вычесть второе или третье. А пятое число поделить на седьмое?” И в результате проведенных над числами операций получаются разные закономерности. Примерно так рассуждал и Архимед: ”Совершенно очевидно, что чем меньше диаметр окружности, тем меньше ее длина. Но нет ли какой-нибудь зависимости между длинами окружности и диаметра?”

Будем действовать подобно Архимеду.

Четвертое исследование: Поиск зависимости между длиной окружности и ее диаметром.

Пусть Черепашка разделит значение длины каждой окружности на длину ее диаметра. Воспользуемся командой ПИШИ.

ПИШИ 360 / 114. Видим на экране результат: 3.1579. Теперь проведем этот эксперимент для окружностей второго, третьего и четвертого размеров.

Итоги исследования:

для ОКРУЖНОСТИ1 - результат деления длины окружности на длину диаметра 3.1579;

для ОКРУЖНОСТИ2 - 3.1579;

для ОКРУЖНОСТИ3 - 3.1579;

для ОКРУЖНОСТИ4 - 3.1579.

Итак мы получили потрясающий результат: Отношение длины окружности к длине диаметра - число постоянное!

Это число называется ПИ. Без этого числа в математике невозможно вычислить длину окружности и площадь круга, а также объем цилиндра, конуса. И это совсем неполный список всех заслуг числа ПИ.

Вопрос 8: А как вычислить длину окружности, если мы знаем длину ее диаметра? Нетрудно догадаться, что надо перемножить число ПИ и диаметр окружности. Вот и еще один результат этого исследования: чтобы вычислить длину окружности, надо длину диаметра умножить на число ПИ.

Пятое исследование: А права ли Черепашка (прав ли Архимед)?

Давайте убедимся, что полученные результаты ни в коей мере не являются только “черепашьими”. Будем действовать так же, как много лет назад действовали современники Архимеда. Воспользуемся подручными средствами: линейкой и куском веревки. Будем измерять нашу любимую кружку.

Вопрос 9: Какую форму имеет кружка?

Чаще всего это цилиндр, у которого верхнее и нижнее основание равны и имеют форму окружности. Давайте измерим длину окружности основания, воспользовавшись древним способом. Наложим на верхнее или нижнее основание кусок веревки и пометим точку соединения. Теперь, чтобы узнать длину окружности основания, достаточно вытянуть кусок веревки по линейке - отмеченная точка укажет на количество сантиметров (24.6 см). Теперь воспользуемся другим способом для вычисления длины этого же основания - с помощью числа ПИ.

Вопрос 10: Что мы должны знать для этого?

Диаметр окружности, который легко измерить с помощью линейки (7.8 см ), значение числа ПИ - 3.1579 и формулу для вычисления длины окружности: чтобы вычислить длину окружности, надо длину диаметра умножить на число ПИ. Воспользуемся командой ПИШИ:

ПИШИ 7.8 * 3.1579. На экране видим результат - 24.6316. Сравним этот результат с результатом, полученным первым способом. Нетрудно заметить, что эти два числа приблизительно равны. Приблизительное равенство получается из-за неточности наших измерений.

Итак, в результате этого исследования мы еще раз убедились в существовании зависимости между длиной окружности и ее диаметром (их отношение есть число постоянное - ПИ) и правильности формулы для вычисления длины окружности.

Попробуйте дома измерить любимую кружку мамы или папы двумя способами и сравните полученные результаты.