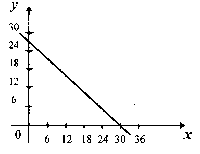|
Шапиро Иосиф Максимович - кандидат педагогических наук, профессор кафедры дидактики математики, Отличник народного образования РСФСР, отличник просвещения СССР, Заслуженный учитель РФ. |
МОТИВАЦИОННАЯ
ФУНКЦИЯ ЗАДАЧ В ОБУЧЕНИИ МАТЕМАТИКЕ Важной проблемой методики преподавания математики является поиск путей совершенствования процесса обучения, активизации познавательной деятельности учащихся. Решение этой проблемы предполагает усиление мировоззренческого аспекта обучения, совершенствование методов реализации прикладной и практической направленности преподавания математики. Среди возможностей решения проблемы видится внедрение в практику работы учителей обучения математике через задачи. Роль задач в обучении математике чрезвычайно велика. Они могут служить многим конкретным целям обучения, выполнять разнообразные дидактические функции. Широкое использование в учебном процессе мотивационной функции задач является одним из средств его активизации. Такое применение задач способствует осознанному восприятию учащимися программного материала, овладению прочными знаниями, развитию мыслительной деятельности школьников. Использование в обучении математике мотивационной функции задач означает, что они могут иметь своей дидактической целью:
Несомненную ценность для мотивации изучения нового математического материала представляют задачи с практическим содержанием. Жизненной необходимостью решения подобных задач наиболее естественно обосновывать потребность в новых математических идеях, знаниях, методах. Акцентирование внимания на необходимости овладения математической теорией под влиянием потребностей практики способствует формированию у школьников научных взглядов. Использование задач для мотивации знаний, умений, методов создает условия для реализации на этапе введения нового учебного материала межпредметных связей, связи обучения математике с жизнью. |
Предварение изучения математической теории постановкой задач предоставляет учителю благоприятные возможности для использования на уроках элементов проблемного обучения. Значимость задач проблемного характера для достижения образовательных, развивающих , воспитательных и практических целей обучения математике переоценить невозможно. Такие задачи могут не только служить средством введения новых понятий и методов, обоснования полезности изучения программного материала. Их использование обеспечивает более осознанное овладение математической теорией, учит школьников самостоятельному выполнению учебных заданий, приемам поиска, исследования и доказательства, основным мыслительным операциям, выделению существенных свойств математических объектов, формирует интерес к предмету. Использование элементов проблемного обучения ставит учеников в условия, вызывающие у них мышление, способное не только автоматически применять заученное, но и открывать для себя новое. Без этого, как убедительно показал известный психолог С.Л. Рубинштейн, не может быть мыслительной активности.
Задачи, используемые для подготовки учащихся к изучению математической теории, следует подбирать так, чтобы их постановка привела не только к необходимости приобретения новых знаний и умений, но и к применению приобретенных под влиянием этой необходимости знаний для решения наряду с поставленной и широкого класса других задач.
Для мотивации изучения математической теории целесообразно применять текстовые задачи, упражнения, практические задания, лабораторные работы, вопросы-задания, имеющие целью поставить ученика в ряде случаев в условия "открытия новой теории", выдвижения гипотез, которые подтверждаются либо опровергаются доказательством.
Нередко оказывается полезным предварить изучение нового математического факта решением известной ученикам задачи и, используя аналогию, обосновать сохранение метода ее решения для новой задачи, решить которую не представляется возможным в связи с недостаточностью математических знаний.
Рассмотрим отдельные примеры использования задач для мотивации
необходимости овладения новой математической теорией.
Пример 1. Изучение умножения десятичных дробей может быть предварено постановкой следующих задач.
Задача А. Цена одного метра ткани 30 рублей. Найдите стоимость 5 метров ткани.
Решение этой задачи известно ученикам начальной школы:
Здесь уместно поставить перед школьниками проблему; как найти стоимость 5 метров ткани, если цена одного метра будет 30,6 рублей? В результате приходим к следующей задаче.
Задача Б. Цена одного метра ткани 30,6 рублей. Найдите стоимость 5 метров ткани.
Пытаясь решить проблему (5 класс), ученики замечают, что новая задача аналогична предыдущей, и естественно находить стоимость ткани умножением цены на число метров, т.е. 30,6 * 5.
Некоторые учащиеся, несомненно предложат заменить 30,6 рублей 3060 копейками, выразить стоимость 5 метров ткани сначала в копейках, а затем их перевести в рубли:
Затем, варьируя числовые данные, учитель формулирует следующую задачу.
Задача В. Цена одного метра ткани 30,6 руб. Найдите стоимость 4,2 метра ткани.
Используя аналогию с решением задач А и Б, ученики приходят к выводу, что
стоимость ткани составит 30,6 * 4,2 (руб.). Однако, довести решение задачи до
числового результата окажется для школьников затруднительным (но не
невозможным) в силу того, что они не владеют правилом умножения десятичных
дробей. Таким образом, потребность в решении подобных задач привела к
необходимости овладения новой математической теорией.
Пример 2. Нахождение суммы внутренних углов выпуклого четырехугольника может быть предварено постановкой следующей лабораторной работы.
Каждому ученику выдается модель фигуры, имеющей форму выпуклого
четырехугольника, причем все модели отличаются друг от друга как формой, так и
размерами. Ученикам предлагается измерить углы четырехугольника и вычислить их
сумму. Выясняется, что сумма углов каждого четырехугольника приблизительно
равна 360 . Выдвигается гипотеза: "Сумма внутренних углов выпуклого
четырехугольника равна 360 ". Доказательство соответствующего предложения
подтверждает справедливость выдвинутой гипотезы.
Пример 3. Введению понятия линейной функции можно предпослать постановку среди других задач - задачи с практическим содержанием.
Задача. Основной месячный заработок рабочего сельскохозяйственного предприятия - 760 рублей. За производство сверхплановой продукции стоимостью в один рубль ему дополнительно выплачивается 19 копеек. Выясните вид зависимости общего месячного заработка рабочего от стоимости произведенной им сверхплановой продукции.
Первоначально необходимо разъяснить учащимся смысл экономических терминов "сверхплановая продукция", "дополнительная оплата труда", "стоимость продукции", после чего решение задачи осуществляется учениками под руководством учителя.
Если обозначить стоимость произведенной рабочим сверхплановой продукции через х рублей, то дополнительная оплата его труда составит 0,19х рублей. Так как общий месячный заработок складывается из основного месячного заработка и дополнительной платы за производство сверхплановой продукции, то общий месячный заработок (у) рабочего выразится формулой у = 760 + 0,19х. С подобной зависимостью школьники встречаются впервые. Ни вид, ни свойства ее им не известны.
Рассмотрев еще примеры задач с практическим содержанием (на выяснение вида
зависимости конечной скорости равноускоренного движения от времени, стоимости
телеграммы от числа слов в ней и другие), учитель вводит понятие линейной
функции, совместно с учениками определяет это понятие, выясняет его свойства.
Существенно заметить, что рассмотренные примеры являются конкретными моделями
линейной функции, обладающими всеми теми свойствами, которые этой функции
присущи.
Пример 4. Введению понятий линейного уравнения с двумя переменными и его решений, ознакомлению школьников с новым для них методом решения таких уравнений может быть предпослано постановка такой задачи с практическим содержанием.
Задача. Требуется проложить водопровод длиной 191 метр к производственному объекту. Для этого располагают трубами одинакового сечения длиной 5 метров и 7 метров. Сколько труб той и другой длины понадобится для прокладки водопровода?
Внешне задача проста и вроде никаких неожиданностей для учащихся не содержит. Однако первая же попытка составить уравнение по условию задачи результата не дает. До сих пор ученики были знакомы с линейными уравнениями с одной переменной. Составить же такое уравнение по условию рассматриваемой задачи нельзя, так как не заданы ни общее число труб, ни зависимость между числом труб длиной 5 м и 7 м. Поэтому естественно замечание учителя о том, что нередко по условию задачи приходится составлять уравнение не с одной, а с двумя переменными. Пользуясь такой возможностью, ученики, обозначив через х число труб длиной 5 м и через у число труб длиной 7 м, приходят к уравнению
Используя полученное уравнение, учитель знакомит учащихся с новым математическим понятием - линейным уравнением с двумя переменными - с участием школьников дает определение этого понятия.
Для решения поставленной задачи следует научиться подобные уравнения решать.
|
|
Возникает необходимость ввести новое понятие - понятие решения линейного уравнения с двумя переменным, которое вводится как упорядоченная пара чисел (х0, у0), обращающая уравнение в верное числовое равенство. В соответствии с требованиями школьной программы на базовом уровне обучения математике сообщается графический метод решения уравнений подобного вида. Таких решений будет бесконечное множество: координаты каждой точки прямой - графика уравнения - являются его решением. |
Однако по смыслу задачи полученный вывод абсурден: число труб не может быть ни отрицательным, ни дробным. Учитывая, что x N и y N надо уточнить, что условию задачи удовлетворяют только координаты тех точек прямой графика уравнения, которые выражаются натуральными числами. Поиск приводит к заключению, что задача имеет 5 решений - пары чисел (34; 3), (27; 8), (20; 13), (13; 18), (6; 23). Но такое число решений задачи прикладного характера практически мало пригодно. Желательно получить единственное решение. Для этого естественно условие задачи дополнить двумя требованиями: 1) трубы разрезать нельзя; 2) число соединений при сварке труб должно быть наименьшим (это экономически выгодно). Нетрудно выяснить, что наименьшее число соединений достигается при х = 6, у = 23.
Следует заметить, что приведенный метод решения задачи не является единственным. Поэтому целесообразно во внеклассной работе по предмету или на уроках в классах с повышенным уровнем обучения математике знакомить учеников с другим методом решения линейных уравнений с двумя переменными с натуральными коэффициентами. Рассмотрим сущность этого метода на примере рассматриваемой задачи.
Так как число 191 не кратно ни 7, ни 5, и учитывая дополнительные
требования к условию задачи, можно сделать вывод о том, что ограничиться
трубами одного из двух заданных размеров нельзя. Запишем уравнение в виде
5х = 191 - 7у. Помня, что х N, у N, воспользуемся признаком делимости чисел на 5.
Решение уравнения сводится к нахождению таких натуральных значений
х и у, при которых (191 - 7у) кратно
5. В результате придем к решениям, полученным выше.
Пример 5. Задания-вопросы проблемного характера могут найти применение для выявления некоторых свойств геометрических фигур.
Как известно, прямая, проведенная через середины двух сторон треугольника, параллельна третьей стороне.
Целесообразно поставить перед учениками следующую серию вопросов (по существу задач на доказательство):
1. Параллельна ли прямая, проведенная через середины двух несмежных сторон: а) параллелограмма; б) квадрата, в) произвольного четырехугольника любой из оставшихся сторон названных фигур?
2. Параллельна ли прямая, проведенная через середины двух смежных сторон: а) параллелограмма; б) квадрата; в) произвольного четырехугольника хотя бы одной из диагоналей названных фигур?
Обсудив ответы школьников, выявляем новые свойства некоторых четырехугольников, оформляем их в виде математического предложения.
Опыт работы значительного числа учителей Алтайского края свидетельствует о
том, что широкое использование мотивационной функции задач в обучении является
эффективным средством повышения качества математической подготовки
учащихся.
Содержание