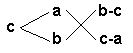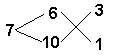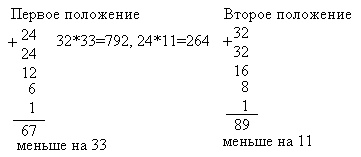Вопросы метрологии на уроках и внеклассных занятиях

Система упражнений метрологического содержания

Сравнение вычислений в различных системах мер.

Примеры подготовки учащихся к решению задач повышенной трудности

Задачи на смешение

Задачи на пропорциональное деление

Метод ложного положения

Нестандарные задачи со старинными русскими мерами

Вопросы метрологии на уроках и внеклассных занятиях

"Решение задач — практическое искусство, подобное плаванию, катанию на лыжах, игре на фортепиано; научиться ему можно только подражая хорошим образцам и постоянно практикуюсь... если вы хотите научиться плавать, то смело входите в воду, если хотите научиться решать задачи, то решайте их ". (Д. Пойа.)

"...сообразительность и "смекалку" нельзя ни "вдолбить", ни "вложить", ни в чью голову. Результаты надежны лишь тогда, когда введение в область математических знаний совершается в легкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащей остроумностью и занимательностью ". (Е.И. Игнатьев).

    Попытки приобщить учащихся к неформальному изучению математики мною предпринимались на протяжении всей педагогической деятельности. Вводились элементы занимательности на уроках, проводились математические соревнования, викторины и т.п. Большую помощь в этом оказывали кружковые занятия. Заметив у ребят возросший интерес к истории отечественной математики, я стала вводить элементы русской метрологии на уроках. Это были устные упражнения, расшифровывающие поговорки и пословицы, загадки или цитаты из литературных произведений.
    О значении устных упражнений на уроках написано немало. Они готовят учащихся к последующим этапам урока: служат и пропедевтикой, и способом повторения материала. Устные вычисления тренируют память, приучают считать рационально. Задачи, решаемые устно, тренируют логическое мышление.
    Одним из видов устных упражнений является перевод единиц измерения.

    В качестве занимательного элемента на уроке приводится одна или несколько русских пословиц или поговорок. Ученики "расшифровывают" их. Вот несколько примеров:
    а) "Мал золотник, да дорог".
    Сначала говорим о значении, смысле этого выражения — что-то маленькое, незначительное на вид и по размерам, но очень ценное, важное. 1 золотник равен 4,3 грамма, действительно, вес невелик, но измеряли в золотниках массу драгоценных металлов и камней.
   Задание. 1 рубль содержал 4 золотника серебра, выразите в граммах массу старинного рубля.
   Решение. 4,3*4=17,2 (г).
    б) Существовал ли когда-нибудь человек "семи пядей во лбу"?
    1 пядь=18 см, 7 пядей= 18*7= 126 см. Ответ отрицательный.
    в) Каков рост, человека, которого прозвали "коломенской верстой"?
    Во время царствования Алексея Михайловича Романова вдоль дороги от Москвы до Коломенского были расставлены на расстоянии 700 саженей друг от друга верстовые столбы, высотой около 4м, с орлами. Впечатление людей было настолько велико, что осталось в народной речи (высота столба 2 сажени =2*2,16=4,32 м).
    1 верста=500саженям=1,08 км, 2,16*500=1080м.
    г) Определите "рост" человека, о котором говорят "от горшка два вершка, а уже указчик" (высоту горшка считать 25 см.).
    1 вершок = 4,5 см, 2 вершка = 4,5*2 = 9 см, 25+9 = 34 см.
    Так говорили о человеке, который, не имел жизненного опыта, самонадеянно о чем-то судившем, поучавшем кого-то.
    д) Куда это, "за семь верст киселя хлебать?"
    1 верста = 1,08 км, 7 верст = 1,08*7= 7,56 км.
    е) Как глубоко видит тот, о ком говорят: "на три аршина в землю видит?".
    1 аршин = 72 см, 3 аршина = 72*3 = 216 см (1 сажень) = 2 м.
    Так говорится о прозорливом, внимательном человеке, от которого ничего невозможно утаить.

Предлагаются задачи для перевода составных именованных чисел. Например:
    а) 2 сажени 2 аршина 2 вершка - сколько вершков? сколько см.?
        2 сажени 2 аршина = 8 аршинов, 8 аршинов 2 вершка = 8*16+2 = 130 вершков, 130*45 =585 (см).
    б) 5 рублей 2 гривны 3 алтына — сколько копеек? (529 коп.).
    в) Сколько золотников в 25 пудах? 25*40*96 = 96000 золотников.
    г) Сколько вершков в версте? Сколько сантиметров?
        1 верста = 500 саженей = 1500 аршин = 24000 вершков,
        24000*4,5 = 90000+18000 = 108000(см).

В виде устных упражнений на некоторых уроках предлагаются задачи, подобные таким:
    а) Двое вышли одновременно навстречу друг другу из двух городов, отстоящих друг от друга на 75 верст. Один проходит в час 4 версты, другой - 3 1/2 .Через сколько часов они встретятся?
   Решение: 75:(4+3 1/2)= 10(ч).
    б) Я за 12 рублей купил 8 фунтов кофе и 4 фунта чаю. Чай втрое дороже, чем кофе. Что стоит фунт того и другого?   Решение:
   1) 8+4*3 = 20 (ф) если бы был только кофе,
    2) 12:20= 0,6 (р) цена одного ф. кофе,
    3) 0,6*3 = 1,8 (р) цена одного ф. чая.
    в) Чиновник получал 500 р. в год. В первые 7 месяцев года он тратил по 45 (р). Сколько может он, не делая долгов, тратить в каждый из остальных месяцев? Решение:
    1) 45*7 = 315 (р) - истрачено денег за 7 месяцев,
    2) 500-315 = 185 (р) - остаток на остальные 5 месяцев,
    3) 12-7=5(м),
    4) 185:5= 37 (р) - ежемесячная трата в остальные 5 месяцев.

    В работе используются некоторые задачи из сборника "1001 задача для умственного счета" (пособие для учителей сельских школ), автором которого является С.А. Рачинский. Они включают в себя не одно, а несколько действий. Учащиеся должны не просто выполнять вычисления, но и подумать над ходом задачи, планом ее решения.
    Условия их интересны и с воспитательной стороны, так как дают возможность сопоставить условия жизни людей разных слоев: зарплаты, затраты, интересы, возможности, масштабы цен и т.д.
    Задачи такого типа можно предлагать учащимся 5-6-х классов при изучении действий с десятичными дробями, при отработке навыков решения задач на движение.
    Для оптимизации вычислительной деятельности предлагаются задачи на смекалку, сообразительность. Обычно они не требуют больших вычислений, решение их нетрадиционно. Поэтому активно участвуют даже слабоуспевающие ученики.
    а) Длина бревна 5 аршин. В одну минуту от этого бревна отпиливают по одному аршину. Во сколько минут будет распилено все бревно? (Распилов будет 4, поэтому ответ — 4 минуты).
    б) Двое крестьян поделили между собой 7 рублей, причем один крестьянин получил, на 3 рубля больше другого. Сколько досталось каждому. ((7-3):2=2; 2+3=5).
    в) Разделить полтину на половину. (50:1/2=100 (к)=1(р)).
    г) В 6 часов утра в воскресенье гусеница начала всползать на дерево. В течение дня, т.е. до 6 часов вечера, она всползала на высоту 5 аршин, а в течение ночи опускалась на два аршина. В какой день и час она поднимется на высоту 9 аршин?
        Часто при решении подобных задач рассуждают так: гусеница в сутки, т.е. в 24 часа, поднимается на 5 аршин без 2-х. Значит всего в сутки она поднимается на 3 аршина. Следовательно, на высоту 9 аршин она поднимется по истечению 3 суток, т.е. она будет на этой высоте в среду в 6 часов утра. Но такой ответ неверен: в конце вторых суток, т.е. во вторник в 6 часов утра гусеница будет на высоте 6 аршин. В этот же день, с 6 часов утра до 6 часов вечера она всползет еще на 5 аршин, т.е. достигнет высоты 11 аршин. Следовательно на высоте 9 аршин она окажется во вторник в 1 час 12 минут пополудни.
        1) 5:12= 5/12 аршин в час,
        2) 3:5/12=36:5= 7 1/5 ч,
        3) 6+7 1/5 = 13 1/5 = 13 часов 12 минут.
    д) Хозяйка в продолжение поста накопила два горшка масла: один в 8 фунтов, другой в 3 фунта. Третий горшок в 5 фунтов остался пустым. Перед праздником хозяйке понадобилось одолжить 6 фунтов масла соседке. Как она это сделала, если меркой могли служить только те же три горшка? (из 8-фунтового отложили в 5-фунтовый 5 фунтов и к оставшимся 3 фунтам добавила 3 фунта из 3-фунтового).
    Задачи со старинными русскими мерами постепенно усложнялись в процессе обучения. Они использовались на различных этапах урока: при повторении, изучении нового материала, при закреплении. Краеведческие задачи и задачи с историческим содержанием имеют расчетный характер, а занимательные задачи требуют особого подхода, смекалки и немалых умственных усилий.
    В начале обучения для учащихся V классов в кабинет вывешивались таблицы перевода старинных русских мер, использовались рисунки. Впоследствии можно было ограничиться лишь переводом наименовании, использованных в тексте задачи. Шестиклассники после значительного количества решенных старинных задач и прослушанных сообщении и докладов из области метрологии запомнили значения основных старинных русских мер.

В начало

Система упражнений метрологического содержания

    В V классе по теме "Натуральные числа и действия с натуральными числами". Закрепляются и развиваются навыки арифметических действии с натуральными числами. Развиваются умения решать задачи на движение, на зависимость между ценой, количеством и стоимостью товара. Решаются задачи арифметическим способом. Например:
   1. "Собака и заяц".
   Собака усмотрела зайца в 150 саженях от себя. Заяц пробегает за 2 минуты 500 саженей, а собака за 5 минут 1300 саженей. За какое время собака догонит зайца? Решение:
       1) 500:2=250 (саж.) - пробегает за одну минуту заяц,
        2) 1300:5=260 (саж.) - пробегает за одну минуту собака,
        3) 260 - 250= 10 (саж.) - за одну минуту сокращается расстояние между зайцем и собакой,
        4) 150:10= 15 (мин.).
        5) Ответ: собака догонит зайца за 15 минут.

    2. Велосипедисты и муха.
    Два города А и В находятся на расстоянии 300 верст друг от друга. Точно в один день, час, минуту, секунду из этих городов выезжают друг другу навстречу два велосипедиста и мчатся, не останавливаясь, со скоростью 50 верст в час. Но вместе с первым велосипедистом из города А вылетает и муха, пролетающая в час 100 верст. Муха обгоняет велосипедиста и летит навстречу другому велосипедисту, выехавшему из города В. Встретив этого, она тот час поворачивает назад к велосипедисту А. Повстречав его, опять летит обратно навстречу велосипедисту В и так повторяет свое летание взад и вперед до той поры, пока велосипедисты не встретились. Тогда она успокоилась и села одному велосипедисту на шапку. Сколько верст пролетела муха "пока успокоилась и села?"
   Решение: Сюжет задачи занимателен, достаточно длинное условие, но суть задачи в том, что муха находилась в полете столько времени, сколько ехали до встречи велосипедисты:
        1) 50*2=100 (верст в час) — скорость сближения,
        2) 300:100=3 (часа) — время до встречи,
        3) 100*3=300 (верст) — пролетела муха. Ответ: 300 верст пролетела муха.

    3. Сколько стоят гуси?
    Некто купил 96 гусей. Половину гусей он купил, заплатив по два алтына и семь полушек за каждого гуся. За каждого из остальных гусей он заплатил по 2 алтына без полушки. Сколько стоит покупка?
       Решение:1 алтын = 3 копейкам = 12 полушкам.
        1) 2 алтына 7 полушек = 12*2+7=31 полушка,
        2) 96:2=48 (гус.) — половина гусей,
        3) 31 *48= 1488 (полушек),
        4) 2 алтына = 24 полушкам, цена гуся из второй половины 24-1=23 (полушки),
        5) 23*48=1104 (полушки),
        6)1488+1104=2592 (полушки) = 2592:4=648 (коп) = 6 руб 48 коп = 6 рублей 16 алтын.
       Ответ 6 рублей 16 алтын.

    4. Сколько куплено баранов?
    Один человек купил 112 баранов старых и молодых, заплатив за них 49 рублей и 20 алтын. За старого барана он платил по 15 алтын и по 4 полушки, а за молодого барана по 10 алтын. Сколько каких баранов было куплено? Решение:
       1) 15*3*4+4= 184 полушки = 46 копеек — стоит старый баран,
        2) 10*3=30 копеек — стоит молодой баран,
        3) 46-30= 16 копеек — разница в стоимости,
        4) 30*112=3360 копеек — было бы уплачено, если бы были куплены только молодые бараны,
        5) 49 рублей 20 алтын = 49 рублей 60 копеек = 4960 копеек — уплачено за всю покупку, 4960-3360=1600 копеек — излишек, который оплатил большую стоимость старых баранов,
        6) 1600:16=100—старых баранов,
        7) 112-100= 12 — молодых баранов.
       Ответ: 100 старых и 12 молодых баранов.
    Эту задачу следует решать после задачи о "фазанах и кроликах". Ее решению можно посвятить внеклассное занятие, рассмотрев несколько способов решения, (см. приложение).

    5. Старшему сыну давали в день 4 копейки, а младшему по 45 копеек в месяц. Но они делили эти деньги пополам. Сколько получил каждый в год?
        1) 4*365= 1460 (к) — получил за год старший сын,
        2) 45* 12=540 (к) — получил за год младший,
        3) 1460+540=2000 (к) — общая сумма,
        4) 2000:2=1000 (к) = 10 (р) — получил каждый.
       Ответ: по 10 рублей.

    При изучении темы "Десятичные дроби. Действия с десятичными дробями" вырабатываются умения выполнять арифметические действия с десятичными дробями, навыки округления десятичных дробей. Решение текстовых задач должно этому способствовать.

    Предлагаются задачи с историческим содержанием:
   1. Белокаменный Кремль, возведенный при Дмитрии Донском, имел стены длиной 916,2саж.Современный Кремль имеет стены на 0,256 км длиннее. Вычислите длину стен современного кремля. 1 сажень=216см=2,1б м (до XVIII в.)
        1) 916,2*2,16=1978,992 м ? 1979 метров = 1,979 км,
        2) 1,979+0,256=2,235 км.
       Ответ: 2,235 км.
    2.Какой высоты была Спасская башня в 1701 году, если известно, что высота ее шатра 5,79 саж., высота башенки в 1,7 раза больше, а высота собственно башни в 2,3 раза больше высоты шатра? (Высоту каждой части башни вычислить с точностью до 0,1 м.). Решение.
        1)Выразим в метрах высоту шатра: 5,79*2,16=12,5064 ? 12,5 м,
        2) 12,5* 1,7=21,25м ? 21,3м — высота башенки,
        3)12,5*2,3=28,75м ? 28,8 м — высота собственно башни,
        4)12,5+21,3+28,8=62,6м.
       Ответ: Высота Спасской башни в 1701 году была 62,6 метра.
   З.Три ядра псковских пушек имели общую массу 160 фунтов, причем масса меньшего из этих ядер составляла 0,25 массы всех трех ядер. Масса наибольшего ядра составляла 0,6 от массы среднего и большего ядер. Вычислить массу каждого ядра. Решение:
        1)160*0,25=40фунтов=1пуд — масса меньшего ядра,
        2)160-40=120 фунтов=3 пуда — масса среднего и большего ядер,
        3)120*0,6=72 фунта — масса большего ядра,
        4)120-72=48 фунтов — масса среднего ядра.
       Ответ: 40ф.,48ф.,72ф.
    Чтобы показать рациональность метрической системы мер решаем задачи на сравнение вычислений в различных системах мер.

В начало

Сравнение вычислений в различных системах мер

    Для иллюстрации того, насколько метрическая система упрощает вычисления, приводим решение одинаковых по смыслу задач в старой русской системе и в метрической системе мер.
   I. Сколько раз 22 пуда 11 фунтов 1 золотник содержатся в 155 пудах 37 фунтах 2 лотах 1 золотнике?
    Задача (пример) решается делением. Делимое и делитель нужно раздробить в наименьшие содержащиеся в них единицы.
        1) 22*40=880 (фунтов),
        880+11=891 (фунт),
        891*96=85536 (золотников),
        85536+1=85537 (золотников);
        2) 155*40=6200 (фунтов),
        6200+37=6237 (фунтов),
        6237*32=199584(лотов),
        199584+2= 199586 (лотов),
        199586*3=598758 (золотников),
        598758+1=598759 (золотников);
        3) 598759 : 85537 = 7.
        Ответ: 7 раз.

    Такой же вопрос в метрической системе:
    Сколько раз 85 килограммов 537 граммов содержатся в 5 центнерах 98 килограммах 759 граммах? Решение:
        1) 85кг 537г = 85527 г,
        2) 5ц 98кг 759г = 598759 г,
        3) 598759:85537 = 7.
    В этом решении первые две строки нет надобности писать, т.к. в метрической системе составное именованное число, состоящее из центнеров, килограммов и граммов можно сразу писать в граммах.

   II. Найти вес чугунной линейки в 1 фут 2 дюйма длины, 2 дюйма ширины и 4 линии толщины, если удельный вес чугуна равен 7 (фут= 12 дюймов, дюйм - 10 линиям)
   Решение: 1) 1 фут 2 дюйма = 14 дюймам, 4 линии = 0,4 дюйма,
        2) Объем линейки 14*2*0,4=11,2 куб. дюйма,
        3) Вес воды того же объема: 3,84*11,2 = 43.008 золотника (Для вычисления веса надо знать, что вес одного кубического дюйма воды равен 3,84 золотника),
        4) Вес линейки 43,008*7=301,056 золотника = 3 фунта 13,056 золотника.

    Такой же вопрос в метрических мерах.
    Найти вес чугунной линейки длиной в 3 дециметра 5 сантиметров, шириной в 4 сантиметра и толщиной в 7 миллиметров; удельный вес чугуна 7.
        35*4*0,7 = 98 куб. сантиметрам.
        Число 98 выражает вместе с тем в граммах вес (массу) воды того же объема, как линейка.
        Вес линейки: 98*7=686 граммам.

    Предложенные выше задачи вызывают интерес учащихся необычностью условия, содержания текста. Кроме того, многие из них могут быть решены несколькими способами. Отдавая предпочтение арифметическим, я стремлюсь к тому, чтобы ребята четко устанавливали связь между данными условия, понимали суть описываемого процесса. Важным условием решения таких задач является пояснение к выполняемым действиям или постановка вопроса к каждому из них. Обращаем внимание и на единицы измерения входящих в условие величин. Все это способствует неформальному подходу к решению текстовых задач.
    Для учащихся VI классов задачи усложняются. Шестиклассники должны научиться выполнять все действия с обыкновенными дробями, с рациональными числами. Для развития логического мышления, для закрепления вычислительных навыков предлагаются задачи с занимательным сюжетом из сборников старинных русских задач [18], [26.] [27], [30], [37], [46], [47].
    Подготовка к решению задач повышенной трудности имеет важное значение. В течение одного или нескольких предшествующих уроков ребятам предлагаются задачи, подобные, но с меньшим количеством данных.
    Рассмотрим примеры подготовки учащихся к решению задач повышенной сложности.

В начало

Примеры подготовки учащихся к решению задач повышенной трудности

    Задача: Разносчик одному покупателю продал 15 яблок и 10 апельсинов и получил с него 1 р. 20 к., а другому продал 15 яблок и 15 апельсинов и получил с него 1 р. 50 к. Почем он продал 10 яблок и 10 апельсинов?
    Разбор задачи начинается вопросом: "О чем говорится в задаче?" (если ученики усвоили содержание прочитанного с первого раза, то вопрос можно не задавать). Дальнейшие вопросы относятся к труднейшей части задачи. Например: почему разносчик со второго покупателя получил больше, чем с первого?
    После ответа учеников, следует новый вопрос:

На сколько именно больше получил разносчик со второго покупателя? 1р.50 к. - 1р.20к. = 30к. (зависимость между
данными раскрыта, значит можно переходить к вычислениям) 15-10=5 (апельсин);

Как узнать цену одного апельсина? 30:5=6 к.;

Почему первый покупатель заплатил 1 р. 20 к., а не 60 к?

Сколько же заплачено за яблоки? 1 р. 20 к. — 6*10=60 к.

Сколько стоит 1 яблоко? 60 к. :15=4 к.;

10 яблок и 10 апельсинов стоят: 60+4*10=1 р.

    Еще задача, вызывающая некоторое затруднение:
    Работник нанят с платою 1 р. 50 к. в день, но с тем условием, что в тот день, когда он не будет работать, он сам будет платить по 30 к. за еду. Через 45 дней он окончил работу и получил всего 54 р. 90 к. Сколько дней он работал и сколько не работал?
    Приступая к разбору, прежде всего необходимо обратить внимание учащихся на получение неполной платы за 45 дней и причины ее уменьшения, т. к. в этом ключ к решению задачи.

Все ли получил работник, что ему следовало?

Почему же не все?

На сколько меньше из-за того, что не работал несколько дней, он получил?

А когда он не работал, на сколько уменьшилась плата?

Было ли условие бесплатно кормить работника, когда он не работает?

На сколько меньше он должен получить если не работал день? Чтобы проверить, на сколько учащиеся усвоили
объяснения, можно задать вопрос: Почему же плата уменьшилась на 1 р. 80 к.?

Скажите, сколько дней работник не работал?
1) 1 р. 50 к. * 45 =67 р. 50 к. —должен был получить за 45 дней работы.
2) 67 р. 50 к. — 54 р. 90 к.= 12 р. 60 к. — общее уменьшение платы.
3) 1 р. 50 к. + 30 к. = 1 р. 80 к. — уменьшение платы за не рабочий день.
4) 12 р. 60 к. : 1 р. 80 к. = 7 (дней) — не работал.
5) 45 — 7 =38 (дней) — работал.

    Решение трудных задач может быть подготовлено решением нескольких более легких, в условии которых меньшее количество данных. Например, подготовить к решению первой из приведенных выше задач можно разбив ее на ряд простых:
    1. Зная цену нескольких одинаковых предметов, как узнать цену другого их числа? Например: За пять апельсинов заплачено 30 к., сколько следует заплатить за 10 апельсинов?
    2. Как по общей цене предметов двух видов узнать цену одного предмета каждого вида, если цена предметов одного вида известна? Например: За 15 яблок и 10 апельсинов заплачено 1 р. 20 к., а апельсины стоят 60 к. Сколько стоит одно яблоко?
    3. Задача, в которой сопоставляются две покупки: За телегу и тройку лошадей просят 155 р., а за ту же телегу и одну лошадь меньше на 90р Сколько стоит одна лошадь?
    Следует обратить внимание ребят на то, за счет чего же стала более дешевой покупка.
    Решение нескольких аналогичных задач подготовит учащихся к решению сложной.

    Для решения второй задачи предлагается предварительно решить ряд задач следующего вида.
    1. Работник в день получает 1 р. 50 к., если же он в какой-то день не работает, то платы за этот день не дают. Через месяц он получил 37 р. 50 к. Сколько с него вычли?
    2. Работник получает в день 1 р. 50 к., если же он в какой-нибудь день не работает, то ему не платят и еще с него удерживается в этот день 30 к. за еду. Сколько получил он через месяц, если работал только 25 дней?
    3. Работник условился работать за 1 р. 50 к. в день, а через месяц получил дишь 37 р. 80 к. Верно ли сделан расчет? Если он получил за 30 дней лишь 37 р. 80 к., сколько с него вычли за все дни?
    4. Работник в день получает 1 р. 50 к. Если он не работает в какой-нибудь день, то плата уменьшается на 1 р. 80 к. за каждый пропущенный день. Сколько дней было пропущено, если за месяц работник получил лишь 37 р. 80 к.?

    Учитель может перефразировать условия, менять числа, но суть каждой из приведенных задач должна быть сохранена.    Задача решается не на одном уроке, в различной форме.
    Роль учителя сводится к тому, чтобы сделать указания и выводы об их решении и значении: в первой задаче обратить внимание на изменение зарплаты, во второй — что плата уменьшается и от вычета, и от удержания поденной платы; в третьей — сравнить действительно полученную плату с причитающейся, в четвертой, как рассчитать по уменьшению заработанной суммы число дней, проведенных без работы.

    Еще один тип задачи, которую можно предложить учащимся... Отцу и сыну вместе 54 года, отцу и деду вместе 104 года, а деду и внуку - 78 лет. Сколько лет каждому?
    При разборе задачи полезно задать вопросы:

Почему отцу и деду вместе больше лет, чем деду и внуку?

Но сколько лет отец старше сына?

Что еще сказано в задаче об их возрасте?

Как узнать этот возраст, если вместе им 54 года, а отец старше сына на 26 лет?

    Запись решения можно вести одновременно с разбором или после повторения всего хода решения.
    Такой подробный разбор трудных задач позволяет принимать участие в ее решении даже тем учащимся, которые не запомнили условие, не поняли его суть.
    Решение:

    1) 104-78=26 (лет)

    2) 54-26=28 (лет) или 54+26=80 (лет)

    3) 28:2=14 (лет) сыну 80:2=40 (лет) отцу

    4) 104-40=64 (года)

    Ответ: деду 64 года, отцу 40 лет, сыну 14 лет.

    Решая задачи повышенной трудности, не ограничиваемся поиском и рассмотрением различных путей решения, но и анализируем, выбираем наиболее красивое решение, более рациональный способ решения.
    Всегда оценивается работа учащихся. Делают это сами ребята. Общее одобрение заслуживают те, кто предложил оригинальный путь решения, показал творческий подход к работе.
    Чтобы учащиеся научились анализировать полученные в ходе решения результаты, предлагается выполнить проверку, с помощью которой еще раз устанавливаются связи между компонентами условия задачи.

    В VI классе предлагаются задачи следующего типа:
    1. Уверяют, что у Эзопа голова была 7 дюймов, а ноги так длинны, как голова и половина туловища; туловище же равно длине ног с головою. Спрашивается рост сего славного человека.
Решение:

    Кратко можно записать условие так:

        голова = 7 д.

        ноги = голове + Ѕ туловища,

        туловище = голове+ ноги,

    Из этой записи виден ход решения:

        туловище=2 головам + Ѕ туловища;

        т.е. 2 головы= Ѕ туловища или

        14д. = Ѕ туловища, откуда

        длина туловища равна 28 дюймам,

        длина ног — 7+14=21 дюйм,

        а весь рост — 7+28+21=56 дюймов=2 аршина,

        в метрической системе: 0,71*2=1,42 м.

    2. Один путник идет от града в дом, а ходу его будет 17 дней, а другой от дому во град тот же путь творяше, может пройти в 20 дней, оба же сии человека пойдоша во един и тот же час от мест своих. Ведательно есть, в колико дней сойдутся? [27]
   Решение: первый путник проходит в день 1/17 всего расстояния, а второй — 1/20, вместе они сближаются за день на 1/17 + 1/20 = 37/340 всего расстояния, значит оба они одолеют все расстояние за 1: 37/340 = 340-37 =9 7/37дня.

    3. Канат длиной 11 аршин разрезали на две части так, что в одной из них оказалось столько вершков, сколько в другой дюймов. Какой длины каждый кусок?
Решение: 1 аршин =16 вершкам=28 дюймам.

    1)11*16=176 вершков длина каната.

    2)16+28=44 — общее число вершков и дюймов

    3)176:44=4 аршина длина меньшего куска.

    4)11-4=7 аршин — больший кусок каната.

Можно решить задачу иначе, составив уравнение:

    Пусть х аршин - длина меньшего куска, тогда длина большего — (11-х) аршин. Их длины должны быть в отношении 16:28 или 4:7.      Составим пропорцию х/(х-1) = 4/7. Решив ее, получим 44-4х=7х, откуда 11 х=44 и х=4.

Ответ: 4 и 7 аршин.

    4. Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. И ведательно есть, в колико дней жена его особенно выпьет ту же кадь.
   Решение: человек вместе с женой выпивает 1/14 часть кади, а с женой 1/10 кади в день. Следовательно жена выпивает в день— 1/10-1/14 = 1/35.Значит всю кадь жена выпьет за 35 дней.
    Старинное решение: за 140 дней человек выпьет 10 бочонков кваса, а вдвоем с женой за 140 дней они выпьют 14 бочонков кваса. Значит, за 140 дней жена выпьет 14-10=4 бочонка кваса. Тогда один бочонок кваса она выпьет за 140:4=35 дней.
    Ответ: за 35 дней.

    5. На мельнице.
    На мельнице имеется три жернова. На первом из них за сутки можно смолоть 60 четвертей зерна, на втором 54 четверти, а на третьем 48 четвертей. Некто хочет смолоть 81 четверть зерна за наименьшее время на этих трех жерновах.
    За какое наименьшее время можно смолоть зерно и сколько для этого на каждый жернов надо зерна насыпать?
   Решение: Ясно, что все три жернова должны работать одинаковое время, потому что простой любого из них увеличивает время помола зерна. За сутки все три жернова могут смолоть 60+54+48=162 четверти зерна, тогда 81 четверть зерна они смелют за 0,5 суток, т.е. за 12 часов. За это время на первом жернове можно смолоть 30 четвертей зерна, на втором 27 четвертей, а на третьем 24 четверти зерна.
   Ответ: за 12 часов,30, 37, 24 четверти зерна.

    6. У помещика было запасено овса больше, чем ржи, на 204 четверти. Когда он продал 32 четверти овса, то осталось овса в пять раз больше, чем ржи. Сколько было ржи и сколько овса?

   Решение.

    1)204-32= 172четв. - разница в количестве ржи и овса после продажи.

    2)5-1=4 частей - разница в количествах.

    3)172:4=43 четверти ржи было у помещика.

    4) 204+43=247 четвертей овса.

    Проверка. 43*5=215 четвертей овса оставалось после продажи.

    215+32=247 четвертей овса было запасено.

    7. Ягодное решето весит 1 3/5 фунта и стоит 16 копеек. Почем за фунт следует заплатить за ягоды, чтобы покупатель не потерпел убытка, принимая решето в общий вес с ягодами, т.е. платя за решето не дороже, чем за ягоды?
   Решение. 1 3/5 фунта= 8/5 фунта — вес решета, а стоит оно 16 копеек, значит цена "одного фунта решета" 16: 8/5 = 10 копеек. Значит и за ягоды надо платить не дороже 10 копеек.

    8. Некто пришел в ряд, купил игрушек для малых ребят: за первую игрушку заплатил 1/5 всех своих денег, за другую 3/7 остатка от первой покупки, за третью игрушку заплатил 3/5 остатка от второй покупки, а по приезде в дом нашел в кошельке денег 1 рубль 92 копейки. Спрашивается, сколько в кошельке денег было и сколько за вторую игрушку денег заплачено?

Решение.

    1) 1 - 1/5= 4/5 всех денег осталось после первой покупки,

    2) 4/5 * 3/7 = 12/35 - часть денег, которую человек заплатил за II игрушку,

    3) 4/5 - 12/35 = 16/35 остаток после двух покупок,

    4) 16/35 * 3/5 = 48/175 - плата за III игрушку,

    5) 16/35 – 48/175 = 42/175 оставшаяся часть денег,

    6)192 : 42/175 = 1050 копеек (10 руб 50 коп) - было в кошельке первоначально,

    7) 1050 * 12/35=360 копеек (3 руб 60 коп) заплачено за вторую игрушку,

Ответ: было в кошельке 4рубля 50 копеек, вторая игрушка стоит 154 2/7 коп.

    9. Продажа двух коней.
    Некто продает двух коней с седлами, из коих цена одного седла 120 рублей, а другого — 25 рублей. Первый конь с хорошим седлом втрое дороже другого с дешевым седлом, а другой конь с хорошим седлом вдвое дешевле первого коня с дешевым седлом. Какова цена каждого коня?
   Решение. По условию стоимость двух коней с седлами в четыре раза больше стоимости второго коня с дешевым седлом и в 3 раза больше стоимости второго коня с хорошим седлом. Значит, разность в стоимости хорошего и дешевого седла, равная 120-25=95 рублям составляет 1/3 – 1/4 = 1/12 части стоимости двух коней с седлами.
    Поэтому кони с седлами стоят 95:1/12=1140рублей. Второй конь с дешевым седлом стоит 1140 * 1/4 =285 рублей, а без седла 285-25=260 рублей. Первый конь стоит 1140-285-120=735 рублей.
   Ответ: 735 и 260 рублей.

    10. Разделить 25 рублей на две части так, чтобы одна часть была в 49 раз больше другой.
   Решение. Вся сумма составляет 1+49=50 частей, значит меньшая часть денег равна 25:50=1/2 рубля — полтина, а большая часть — 25-1/2=24 1/2рубля.
   Ответ: 24рубля 50 копеек и 50 копеек.

    Целый урок может быть посвящен решению задачи Л.Н.Толстого.
    Известный профессор физики А.В.Цингер в своих воспоминаниях рассказывает, что Льву Николаевичу Толстому нравилась следующая задача:
    "Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня вся артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру, вторая же половина артели косила малый луг, на котором к вечеру еще остался участок, который один косарь скосил за день. Сколько косцов было в артели?
    Эту задачу можно решить как арифметически (но требуется, как всегда при арифме-тическом решении задач, догадка), так и алгебраическим способом, при помощи уравнения.
    Сначала попробуем обойтись без уравнений, применив геометрию. Изобразим оба луга в виде двух прямоугольников, один из которых в два раза больше другого. Больший прямоугольник изображает большой луг, а меньший — малый луг.

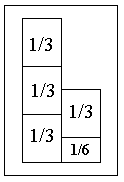
    Чтобы скосить большой луг, вся артель работала первую половину дня, а вторую половину дня работала половина артели. Иначе говоря, половине артели нужно было бы работать трижды по Ѕ дня, чтобы скосить больший луг (все косцы считаются одинаково сильными). Таким образом, половина артели в половину дня скосила 1/3 большого луга.
    Так как меньший луг, представляющий половину большего, составляет 1/3+1/6 большего луга (принимая больший луг за 1=1/3+1/3+1/3, имеем для величины меньшего луга 1/2=1/3+1/6) и во вторую половину дня половина артели на нем скосила одну треть большего луга, то остался нескошенным в конце дня участок, равный одной шестой части большего луга. По условию задачи этот остаток может скосить один косец за день.
    Вся артель за день скосила весь большой луг и часть меньшего, равную 1/3 или 2/6 частям большого луга; следовательно, артель за день скосила всего 1+2/6=6/6+2/6=8/6 частей большого луга. Так как один косец за день может скосить 1/6 часть большого луга, то для того, чтобы скосить за день 8/6 частей большого луга, артель должна состоять из 8 человек.

    Решим эту задачу алгебраически:
    I. Пусть х - число косцов артели, у - размер участка, скашиваемого одним косцом за один день. Заметим, что у - вспомогательная переменная, которая введена для облегчения решения задачи (от нее потом освобождаются).
    Выразим через х и у площади большого и малого луга. Площадь большого луга равна (xy)/2 + (xy)/4 = (3xy)/4, площадь малого луга (xy)/4 +y = (xy+4y)/4, Больший луг по условию в два раза больше малого поэтому (3xy)/4 : (xy+4y)/4=2 или (3xy) / (xy+4y)=2, сократив на y, получим 3х/(х+4)=2, (3х-2х-8)/(х+4)=0, х-8=0, х=8.

    II. Пусть число косцов будет х. Оба луга были скошены при работе всей артели в течение дня и еще одного косца в течение второго дня. Чтобы скосить оба луга потребовалось одному косцу (х+1) день. Чтобы скосить малый луг, составляющий 1/3 обоих лугов, требуется (х+1)/3 рабочих дней. С другой стороны, для того, чтобы скосить малый луг, половина артели работала половину дня (т.е. х/2 косцов, 1/2 дня) иными словами, требовалась работа за х/4 рабочих дня и одного косца за целый день, так что всего косьба малого луга потребовала (х/4 + 1) рабочих дней. Значит, (х+1)/3 = х/4 + 1, х+4=12, х=8.

    III. Установив, что косьба обоих лугов потребовала (х+1) рабочих дней, мы можем найти два выражения для числа дней работы на большем лугу и, приравняв эти выражения, получить уравнение для определения х.
    Так как большой луг составляет 2/3 обоих лугов, то его можно было скосить в 2(х+1)/3 дней. Косила же его вся артель 1/2 дня, что дает х/2 рабочих дней; и половина артели 1/2 дня, что дает еще х/4 рабочих дней; всего для того, чтобы скосить большой луг, потребовалось (х/2 + х/4) рабочих дней. Имеем уравнение: 2/3*(х + I) = х/2 + х/4, 2/3*х+2/3=3х/4, 3х/4-2/3*х=2/3, х/12=2/3, х=8

    Решению задач арифметическими способами уделяется большое внимание именно в V-VI классах для того, чтобы приучить учащихся к рассказу о предполагаемом ходе решения. Это развивает в детях способность давать себе отчет о целой задаче, следить за последовательностью вычислений и приучает предварительно обдумывать свою работу.
    Однако при этом не забывается и алгебраический метод решения текстовых задач. Некоторые задачи решаются для сравнения и тем, и другим способами, а затем делается вывод о наиболее рациональном из них в данном случае.
    Задачи, решаемые на уроках, служат не только развитию сообразительности, они способствуют развитию навыка применять полученные знания к решению вопросов, которые возникают в ходе учебной и трудовой деятельности школьников.
    Уроки не дают такого простора для разнообразной познавательной деятельности, какой возможен на внеклассных занятиях. Более разнообразные формы организации и проведения занятий, отсутствие жестких временных рамок позволяют максимально использовать интересы и способности подростков.
    Более обширный материал с использованием старинной русской метрологии предлагается на внеклассных занятиях. Здесь мы изучаем старинные русские меры длины, объема, веса, денежную систему России прошлых веков, решаем старинные задачи и забавы, разгадываем загадки и кроссворды, изучаем старинные способы решения задач.
    В старинных русских учебниках математики, начиная с "Арифметики" Л.Ф.Магницкого, были помещены многочисленные правила решения задач, и каждый ученик обязан был их знать и применять. Эти правила почти не используются в наше время (кроме "правила смешения", которое с успехом применяется и поныне в при решении химических задач под названием "правила конверта").
    На факультативных занятиях в VI классе мы рассмотрели некоторые из способов решения задач, которыми пользовались в прошлые века, сопоставили их с современными, обсудили возможность их применения. Вот некоторые из них.
    Основой всех практических правил с арифметической точки зрения является понятие о пропорциональности величин и учение о пропорциях.
    В русских математических рукописях и в "Арифметике" Л.Ф. Магницкого отдельной главы о пропорциях нет. Само слово "пропорция" употребляется в житейском смысле, означая соразмерность, соотношение: "пропорция дому", "о пропорциях руд" и т.п. Л.Ф. Магницкий не считал возможным в арифметике пользоваться этим геометрическим методом. Наше понятие "пропорциональность величин" Л.Ф. Магницкий передает словами "подобие", "подобность".
    Ученик Л.Ф. Магницкого Н.Г. Курганов вводит и при решении задач на тройное правило пропорции, замечая, что этот прием есть то "что геометры называют пропорцией".
   Тройное правило.
   Устанавливается правило письма данных в задачах, и после этого решение задач сводится к механическим умножениям и делениям.
    У старых авторов и Л.Ф. Магницкого это правило называется строкой, т.к для механизации вычислении данные писались в строку. Для величин прямо пропорциональных следовало писать данные в одном порядке, для величин обратно пропорциональных — в другом (правило называлось тройным, т.к. в строку записывались три известных числа из условия задачи).
    Примеры:
    1) За 2 рубля можно купить 6 предметов. Сколько их можно купить на 4 рубля? 2 - 6 - 4. Перемножая второе и третье числа и деля произведение на первое, получаем ответ (6*4:2= 12 (пр.)).
    2) 20 рабочих могут выполнить работу в 30 дней. Сколько рабочих могут сделать ту же работу в 5 дней? 5 — 20 — 30 Снова умножаем второе число на третье и делим произведение на первое число 20*30:5= 120 (р)
    Правильность механического решения зависит целиком от правильности записи данных задачи. Поэтому Л.Ф. Магницкий в конце раздела говорит:
    А смотри всех паче
    Разума в задаче,
    Потому бо знати,
    Как сие решати.

В начало

Задачи на смешение

    Старинный способ решения задач на смешение двух веществ позволяют получить правильный ответ.
    Предположим, что смешиваются два вещества — первое стоимостью а гривен за фунт и второе стоимостью b гривен за фунт. Желательно получить вещество стоимостью с гривен за фунт. Будем считать, что а<b (если с>b или с<а, то задача неразрешима, ибо смешивая дешевые вещества, дорогое не получишь).
    Поэтому можно считать, что а<с<b. Смешаем один фунт первого вещества и q фунтов второго. В результате получится 1+q фунтов вещества стоимостью а+bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство а+bq=с*(1+q). Отсюда находим q=(с-а):(b-с). Вещества нужно мешать в соотношении 1 : (c-a)/(b-c) или (b-с):(с-а). Именно это соотношение дает старинный способ



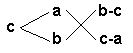
    1. У некоторого человека были продажные масла: одно ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла стоимостью 7 гривен?
   Решение: Друг над другом пишутся стоимости имеющихся масел, слева от них и примерно посередине - стоимость масла, которое должно получится после смешения. Соединив записанные числа черточкми, получим такую картину:

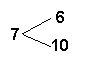
    Меньшую цену вычтем из цены сешанного масла и результата поставим справа от большей цены. Затем из большей цены вычтем цену смешанного масла и запишем справа от меньшей цены. Получим такую картину:

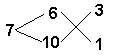
    Делаеться заключение, что дешевого масла неужно взять втрое больше, чем дорогого, т.е. для получения одного ведра масла ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого - 3/4 ведра. (Проверка: 1/4*10+3/4*6=28/4=7 гривен)

    2.Некто имеет серебро разных проб: одну — 12 пробы, другое — 10 пробы, третье — 6 пробы. Сколько какого серебра надо взять, чтобы получить 1 фунт серебра 9 пробы?
    Решение: запишем схематически

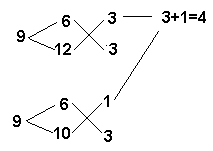
Отсюда следует, что надо взять 4/10 фунта серебра 6 пробы, 3/10 фунта серебра 10 пробы и 3/10 фунта серебра 12 пробы.

    3. Имеет некто чай 3-х сортов — цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти три сорта, чтобы получить чай по 6 гривен за фунт?
Вот решение из "Арифметики" Л.Ф.Магницкого: "А когда случится мешати три товара из них же сделати четвертый по желаемой цене и тогда един перечень малейший дважды в правиле полагается. Яко же эдесь видимо есть:

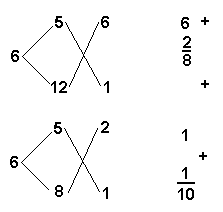
    Здесь предлагается взять 6+2=8 частей чаю ценою по 5 гривен и по одной части чая ценой 8 гривен и 12 гривен за фунт.
    Указанный Л.Ф.Магницким способ состоит в следующем. Надо дважды применить способ записи исходных данных и необходимых количеств веществ, причем в первый раз взять вещества с большей и меньшей стоимостью, а во второй раз с наименьшей и средней стоимостью. Повторив действие вычитания и соответствующей записи разности, получим доли, в которых нужно смешивать вещества наибольшей и средней стоимости (на соответствующих строках). Сложив доли дешевого вещества, найденные в первый и второй раз, получим долю дешевого вещества в общей смеси.

4. Имеется серебро: одно 11 пробы, а другое 14 пробы. Сколько какого серебра надо взять, чтобы получить 1 фунт серебра 12 пробы?

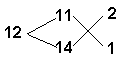
2/3 фунта серебра 11 пробы и 1/3 фунта серебра 14 пробы.

    В России существовала золотниковая система обозначения пробы на основе русского фунта, содержащего 96 золотников, по которой проба выражалась весовым количеством благородного металла в 96 единицах сплава, например, слова "серебро 11 пробы" означают, что в 96 частях сплава содержится 11 частей серебра.
    В наше время проба обозначает число частей благородного металла в 1000 частях (по массе) сплава.

    Задачи на смешение трех веществ могут иметь не единственное решение.
    Предположим, что смесь, составленная из а фунтов цейлонского чая, b фунтов индийского и с фунтов китайского чая имеет цену 6 гривен за фунт. Тогда

5а+8b+12с
————— = 6     или а=6с+2b.
а+b+с

    Значит эта смесь может быть получена соединением смесей I (цейлонский и китайский в отношении 6:1) и II (цейлонский и китайский в отношении 2:1), в отношении с:b.

5. Современная задача на смешение тоже может быть решена этим старинным способом: Имеются два раствора 68% и 78%-ной серной кислоты. Сколько надо взять каждого раствора, чтобы получить 100г. 70% -ного раствора серной кислоты?

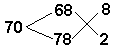
Надо взять 80г. 68% кислоты и 20 г. 78% -ного раствора серной кислоты.

В начало

Задачи на пропорциональное деление

    Такие задачи Л.Ф. Магницкий решает "золотой тройной строкой". Многие из них представляют интерес или по содержанию, или по забавной форме.
    1. "Един человек выпьет кадь пития в 14 дней, а со женою выпьет тое же кадь в 10 дней, и ведательно есть, в колико дней жена его особно выпьет тое же кадь?"
   Решение: За 140 дней человек выпьет 10 бочонков кваса, а вдвоем с женой за 140 дней они выпьют 14 бочонков кваса. Значит, за 140 дней жена выпьет 14-10=4 бочонка кваса, а тогда один бочонок кваса она выпьет за 140:4=35 дней.
    2. "Некий человек нашел работника на год, обещав ему дати 12 рублей и кафтан. Но той, по случаю, работав 7 месяцев, восхотев отойти и прошаше до-стойныя оплаты с кафтаном. Он же даде ему по достоинству расчет 5 рублев и кафтан, ведательно есть: коликой цены оный кафтан был.
   Решение 1. Работник не доработал у хозяина 5 месяцев и недополучил Т рублей; значит, месячная его плата в денежном выражении 7/5 рубля или 1 рубль 40 копеек. Плата за 7 месяцев составит 7* 7/5 = 49/5 =9 4/5 рубля или 9 рублей 80 копеек. Но работник за это время получил 5 рублей и кафтан. Значит, кафтан стоит 4 рубля 80 копеек.
   Решение II. За год работник должен был получить 12 рублей и кафтан, т.е. за каждый проработанный месяц ему должны начислять 1 рубль и 1/12 стоимости кафтана. За проработанные 7 месяцев работник должен был получить 7 рублей и 7/12 стоимости кафтана, а получил 5 рублей и кафтан. Следовательно, 5/12 стоимости кафтана соответствуют 2 рублям. Таким образом, цена кафтана была 2 : 5/12 = 24/5 = 4 4/5 (рубля).

В начало

Метод ложного положения

    С самой глубокой древности и до XIX в руководствах по арифметике занимал очень видное место так называемый метод ложного положения или метод предположений. Долгое время этот метод заменял применение уравнений первой степени при решении задач, приводимых к этим уравнениям. Л.Ф. Магницкий называет раздел своей "Арифметики", трактующей этот вопрос "О правилах фальшивых или гадательных".
    В русской учебной литературе "фальшивое правило" имеется во всех руководствах ХУШв. и в значительной части учебников XIX в. Пример расположения вычислений при применении "фальшивого правила" у Л.Ф. Магницкого: "Спросил некто учителя: сколько у тебя в классе учеников, так как хочу к тебе в ученики отдать своего сына. Учитель ответил: если придет учеников столько же, сколько имею, и полстолько и четвертая часть и твой сын, тогда будет у меня учеников сто." Удивившись ответу, спрашиватель отошел и стал изыскивать посредством сей науки так:

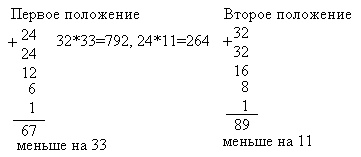
    "Через второе фальшивое правило" 792:22=36 Толико бяше в том училище учеников.

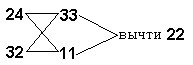
    В первом столбце подсчитывается, что при первом предположении (учеников было 24), мы получили всего 67, меньшее чем 100 на 33. Во втором столбце таким же образом находится, что при втором предположении, что учеников было 32, получается 89, меньше на 11.
    Л.Ф.Магницкий пишет: "Через второе фальшивое правило", т.е. имеем тот случай, когда оба положения дали "меньше". В середине он выписывает оба положения и оба отклонения. Тут же крестом указывает, какое число на какое надо умножить и выполняется умножение 32*33=1056 и 24*11=264, 1056-264=792 и указывается, что по "второму фальшивому правилу" надо найти разность отклонений 33-11=22 и способом вычерчивания выполняетс яделение 792:22=36. "Толико бяше в том училище учеников".
   По "методу весов" решение располагалось бы так. Даем три решения при следующих положениях:

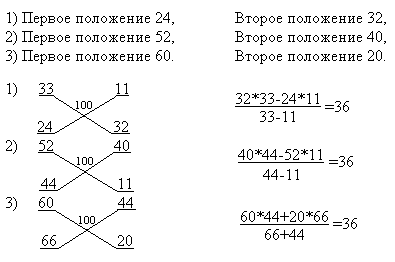
    Правило решения можно записать так: "Возьми для неизвестного числа, какое ты хочешь, назови его "первое положение" и поступай согласно условию задачи. Если оно подходит к условию, то это и есть неизвестное, но если оно отклоняется в ту или другую сторону, назови разницу первым отклонением. Тогда возьми другое число и назови вторым положением; если оно не удовлетворяет условию, то даст второе отклонение. После этого умножай первое положение на второе отклонение и назови произведение первым результатом; затем второе положение умножай на первое отклонение и это есть второй результат. Если оба отклонения в одно и тоже время больше или оба меньше, дели разность двух результатов на разность двух отклонении; если дело обстоит иначе, дели сумму двух результатов на сумму отклонений; частное и есть искомое число.
    С помощью "весов" на одну чашу "клали" первое положение, подсчитав отклонение, писали его над весами, если оно положительное, и гад весами, если оно отрицательное. Если отклонения оказывались записанными оба по одну сторону весов, то накрест взятые произведения положения и отклонения вычитали одно из другого и разность делили на разность отклонений. Если же отклонения оказывались записанными по разные стороны от весов, от произведение и отклонение складывали. Над точкой опоры весов писали требуемую условием правую часть равенства. Старинные русские меры сменились в России в начале XX века метрической системой. Преимущество последней школьники видят при решении задач определенного типа (см. приложение).
    Сравнение громоздких, трудно запоминающихся правил решения задач из старинных учебников математики с современными, теми, которые применяются и на уроках в школе, позволило ребятам сделать вывод о преимуществе алгебраического метода решения задач такого типа.
    Внеклассные занятия дают больше возможностей для развития школьников. На таких занятиях нет жестких временных рамок и строгой регламентированности урока. Каждый ученик выбирает столько заданий, сколько ему под силу, уровень сложности задач тоже можно выбирать. У ребят нет страха, что поставят плохую оценку за неправильное решение. Каждый имеет право на ошибку, поэтому в поиске пути решения задач участие принимают все.
    Задачи для каждого занятия подбираются в соответствии с программой фа-культатива. Уровень их сложности различен: от устных, решаемых почти без вычислений, до таких, на решение которых затрачивается все время, отведенное на занятие. Как правило, это задачи, решаемые и арифметическим и алгебраическим способами. Содержание условия задач интересно для ребят, необычен язык, форма изложения, наименование единиц измерения, поэтому в поиск решения отправляются все. Интерес стимулирует к преодолению трудностей, воспитывает волевые качества личности, трудолюбие, а успех (у каждого свои успехи и достижения) помогает в учении.

В начало

Занимательные, нестандартные задачи со старинными русскими мерами служат хорошим материалом для дополнительной нагрузки, для развития умственных способностей сильных учеников и для тех, кто не силен в математике. Их содержание позволяет учителю расширить кругозор школьников не только в познавательном аспекте (знание истории отечественной математики, условий жизни и быта предшествующих поколений), но и помогает воспитывать их в духе патриотизма.
Рассматривались задачи следующего типа.

Меры длины

    1. Сбор яблок. На расстоянии аршина одно от другого лежат в ряд 100 яблок. Перед первым яблоком стоит корзина, также на расстоянии 1 аршина от него. Спрашивается: какой путь совершит тот, кто возьмется собрать все эти яблоки так, чтобы брать их последовательно одно за другим и каждое отдельно носить в корзину, которая все время стоит на одном и том же месте?
   Решение. Нужно подойти к каждому яблоку и возвратиться обратно к корзине. Значит, число пройденных аршин будет равно удвоенной сумме первых ста чисел, или сто раз взятое число 101, т.е. 10 100 аршин. Это составляет почти семь верст, как видим, способ сбора довольно утомительный.

    2. Длинная борода. Борода у человека растет, удлиняясь в неделю на 1/5 дюйма. Предположим, что борода растет с постоянной скоростью на протяжении всей жизни человека. Какой длины достигла бы борода у мужчины, который не брился в течение 30 лет?
   Решение. В году 52 недели, в 30 годах их 52*30=1560. За это время борода увеличится на 1560:5=312 дюймов=36 футов=3сажени5футов. ( 1 сажень=7 футам=84 дюймам).
    В метрической системе: 312*25,4=7924,8 мм » 7,92 м.

    3. Собака никогда не догонит старика (софизм).(Русский вариант задачи об Ахиллесе и черепахе).
    Собака бежит в 10 раз скорее старика, который находится впереди нее на 100 саженей. Спрашивается, когда собака догонит старика?
    Приводим такое рассуждение: когда собака пробежит 100 саженей, старик будет находиться впереди нее на 10 саженей. Когда она пробежит и эти 10 саженей, то все-таки не догонит старика, который за это время успеет переместиться на 1 сажень. Тогда собака, чтобы догнать старика, должна будет пробежать 1 сажень, но старик, в свою очередь, переместится на 0,1 сажени и т.д.
   Решение. Сложив пути, пройденные стариком, получим 10+1+0,1+0,01+... =11,111... сажени, т.е.
11 1/9сажени. Конечно, собака, пробежав это расстояние, поравняется со стариком, а потом и обгонит его.

    4. Покупка сукна.
   Куплено сукна полторажды полтретья аршина. Заплачено полчетвертажды полпята рубля. Спрашивается, сколько должно заплатить за полсемажды полдевята аршина того же сукна?
   Решение.

Полторажды

полтретья

полчетвертажды

полпяты

1,5

2,5

3,5

4,5

1) "полторажды полтретья" — 3/2 * 5/*2 = 15/4 (арш.)

2) "полчетвертажды полпята" — 3 1/2 * 4 1/2 = 7/2*9/2 = 63/4 (руб.)

3) За 15 аршин заплатили 63 рубля, за 1 аршин — 63/15=21/5 (руб.).

4) "полсемажды полдевята"— 6 1/2 * 8 1/2 = 13/2 * 17/2 = 221/4 (арш.)

Ответ. За покупку надо уплатить 232 рубля 5 копеек.

(Для более простого запоминания: значение известного нам "полтора" происходит от старинного "полвтора").

Мера объема, веса, массы.

    1. Покупка масла.
    Некий человек покупал масло. Когда он давал деньги за 8 бочек масла, то у него оставалось 20 алтын. Когда стал давать за 9 бочек масла, то не хватало денег полтора рубля с гривною. Сколько денег было у этого человека?
   Решение. Девять бочек с маслом стоят на полтора рубля с гривною, т.е. на 16 гривен, больше суммы имеющихся денег, а эта сумма на 20 алтын (6 гривен) больше стоимости восьми бочек. Значит, одна бочка масла стоит 16+6=22 гривны.
    Когда человек давал деньги за 8 бочек масла, у него оставалось 6 гривен, значит до покупки у него было: 22*8+6=182 гривны или 18 рублей 20 копеек.
   Ответ: 18руб.20коп.

   2. Ехали два крестьянина и нашли три бочонка: один восьмиведерный с вином, другой пятиведерный пустой, третий — трехведерный — тоже пустой. Крестьяне задумали поделить вино поровну тут же, на месте с помощью этих трех бочонков, не прибегая к иной посуде. Как же они разделили вино?
   Решение. Крестьяне поделили вино с помощью двух пустых бочонков в результате 7 переливаний, получив по 4 ведра вина каждый.

	восьмиведерный	пятиведерный	трехведерный
до переливания	8	0	0
после первого переливания	3	5	0
после второго	3	2	3
после третьего	6	2	0
после четвертого	6	0	2
после пятого	1	5	2
после шестого	1	4	3
после седьмого	4	4	0

    3. В двух бочках 57 ведер воды; если из первой бочки перелить во вторую 5 ведер, то в первой окажется воды вдвое больше, чем во второй. Сколько воды в каждой бочке?
   Решение. Определим количество ведер воды после переливания. Так как при переливании общее число ведер воды не изменилось, то задача сводится к тому, чтобы число 57 представить в виде двух слагаемых, одно из которых вдвое меньше другого. Меньшее слагаемое будет 57:3=19, а большее 19*2=38. Значит в первой бочке было до переливания 38+5=43 ведра, а во второй — 19-5=14 ведер.
    Эту же задачу можно решить, составив уравнение, что будет проверкой правильности арифметического решения.
   Ответ: 43 и 14 ведер.

Денежная система.

    1. Портниха берет за работу платья 6 рублей. Без помощи машинки она может сшить его за 5 дней, на машинке же — в 3 дня. Во сколько времени окупится машинка стоимостью 48 рублей?
   Решение. Если бы портниха шила вручную, то зарабатывала бы в день 6:5= 1,2 рубля, при работе на машинке она получит 6:3=2 рубля в день. Значит, машинка окупится за 48:(2-1,2)= 60 дней.
   Ответ: за 60 дней.

    2. Веселый француз.
    Веселый человек пришел в трактир с некоторой суммой денег и занял у содержателя трактира столько денег, сколько у себя имел. Из этой суммы истратил 1 рубль. С остальными пришел в другой трактир, где занял денег столько, сколько имел. В этом трактире также истратил 1 рубль. Потом пришел в третий, четвертый трактиры и повторил то же самое. Наконец, когда вышел из четвертого трактира, не имел ничего. Сколько денег имел первоначально веселый человек?
   Решение. Эта задача относится к числу решаемых с конца. Так как после выхода из четвертого трактира у человека не было денег, а истратил он 1 рубль, то после выхода из третьего трактира у него было 50 копеек. Там он истратил 1 рубль, значит перед этим с займом имел 1руб.50коп., т.е.уходя из второго трактира, он имел ровно половину этой суммы 150:2=75 копеек.
    Аналогично, после ухода из первого трактира он имел (100+75):2=87 копеек и 2 полушки. Значит он пришел в первый трактир, имея (87,5+100):2=93 3/4 копейки или 93 копейки и 3 полушки.
   Ответ: 93 копейки 3 полушки.

    3. Хозяин послал работника на базар купить 20 птиц: гусей, уток и малых чирков. Он дал работнику 16 алтын. Гусей велел купить по 3 копейки за штуку, уток — по копейке, а малых чирков — по 2 на копейку. Сколько гусей, уток и чирков купил работник?
   Решение. Работник, отправившись на базар имел 16*3=48 копеек. Так как за гуся ведено платить по 3 коп., то взятых денег хватит на 16 гусей, но тогда нельзя будет купить ни уток, ни чирков. Итак, работник купил не более 15 гусей.
    Допустим, что работник купил чирков и уток. Если бы гуси стоили по одной копейке, то за всю покупку работник заплатил бы меньше 20 копеек и у него осталось бы больше 28 копеек. Эти оставшиеся копейки работник должен потратить на гусей, доплатив за каждого гуся по 2 копейки. По условию работник израсходовал все деньги, значит он купил более 14 гусей. Из всего сказанного следует, что работник купил ровно 15 гусей, потратив на них 45 копеек. Оставшиеся 3 копейки он должен потратить на 5 чирков и уток. Если бы чирки стоили по одной копейке, то покупка обошлась бы 5 копеек. Лишние (5-3=2) две копейки возникли потому, что пришлось бы переплатить за каждого чирка по 1/2 копейки. Поэтому было куплено 4 чирка, а значит 1 утка.
    Итак: 15 гусей, 1 утка, 4 чирка.

    4. Четыре купца.
   Четверо купцов имеет некоторую сумму денег. Известно, что сложившись без первого, они соберут 90 рублей, сложившись без второго — 85 рублей, сложившись без третьего — 80 рублей, сложившись без четвертого — 75 рублей. Сколько у них денег?
   Решение 1. Если из первой суммы (II+III+IV) вычесть деньги второго купца, добавить деньги первого, то вместо 90 получится 85 рублей. Значит у I купца денег на 5 рублей меньше, чем у II. Аналогично рассуждая, можно увидеть, что у III купца на 5 рублей больше, чем у II. Значит I, II, III купцы, сложив деньги вместе соберут втрое больше, чем имеется у II купца. В условии сказано, что эта сумма составляет 75 рублей. Значит, у II купца 25 рублей, у I — 20 рублей, у III — 30 рублей, тогда у IV — 35 рублей.
   Решение 2. Предположим, что I, II и III купцы положат на стол третью часть имеющихся у них денег, т.е. 25 рублей. Затем пусть I, II и IV положат третью часть от первоначально имевшихся у них денег, тогда добавится 80/3 рублей. На столе станет 25 + 80/3 = 51 2/3 рублей. Затем к этой сумме добавят свою треть I, III и IV, и, наконец, II, III и IV. На столе окажется 25 + 80/3 + 85/3 +30 =110 рублей, а купцы останутся без денег.
    Общая сумма 110 рублей, тогда у I купца 110-90=20 рублей, у II — 110-85=25 рублей, у III — 110-80=30 рублей, а у IV — 110-75=35 рублей. Ответ: 20, 25, 30, 35 рублей.

Дележи

1. Как поделить. Два крестьянина, из которых один имел с собой 5 хлебов, а другой три хлеба, встретили на дороге незнакомца. Последний просил дать ему хлеба/ Все трое сели завтракать и съели все 8 хлебов. Незнакомец дал за это 8 рублевиков. Сколько должен получить каждый из двух крестьян?

Решение

    1) 8*3=24 (р) стоили все три хлеба( вклад каждого по 8 рублей)

    2) 24:(5+3)=3 (р) стоит 1 хлеб;

    3) 5*3=15 (р) израсходовал тот, кто внес 5 хлебов;

    4) 15-8=7 (р) ему должны вернуть;

    5) 3*3=9 (р) трата того, кто внес 3 хлеба;

    6) 9-8=1 (р) ему должны вернуть.

Ответ: 7 и 1 р.

    2. Некто купил вещь, заплатив за нее 157 рублей 50 копеек, причем платил одинаковым числом рублевых монет и полтинников. Сколько было полтинников?
   Решение: 157 рублей равно 314 полтинникам. Если бы покупатель давал по два полтинника вместо рублевой монеты, то по условию задачи, ему пришлось бы дать продавцу втрое больше полтинников, чем он дал в действительности. Значит количество полтинников, отданных покупателем, равно 315:3=105, столько же было отдано и рублевых монет.
   Ответ: 105 монет.

Поучительная задача из "Арифметики" Л.Ф.Магницкого.

    Некий человек продал коня за 156 рублев; раскаявшись, купец начал отдавать продавцу, говоря, что конь не достоин такой высокой цены. Продавец предложил ему иную куплю, говоря: "Если тебе кажется, что цена коню высока, то купи только гвозди, которые у коня в подковах, коня же возьми даром, а гвоздей в каждой подкове 6. За первый гвоздь дай мне полушку (1/4 копейки), за другой две полушки, за третий копейку, за четвертый две копейки и т.д. за все гвозди." Купец, полагая, что все гвозди обойдутся не свыше 10 рублев, восхотел коня в дар получить и согласился на такую цену. Ведательно есть, коликим купец — он проторговался.
    Решение: согласно условию покупатель должен был уплатить
    1/4+1/2+1+2¹+2²+2³+2⁴+...+2²¹ копеек (6*4= 24 гвоздя). Всего 4194303 3/4 копейки вместо первоначально спрошенной суммы 156 рублей (15600 копеек).
   Ответ на вопрос задачи "коликим купец — он проторговался", т.е. сколько покупатель потерял бы по сравнению со спрошенной ценой будет 4194303 3/4 - 15600 = 4178703 3/4 копейки =41787рублей 3 копейки 3 полушки.
    На таких условиях не обидно и лошадь дать в придачу. Сам Л.Ф.Магницкий не без основания снабдил решение своей задачи предупреждением:

"Хотяй туне притяжати,

От кого что приимати,

Да зрит то себе опасно,

Чтобы взяти не напрасно,

С тем бо своя истеряет,

Многократно измеряет."

    Последовательное осуществление органической связи между повседневной учебной работой и внеклассными занятиями позволяет добиваться определенных успехов. Обнаружить это возможно , когда учащиеся решают предложенные им новые, ранее не встречавшиеся задачи, совершенно оригинальным способом, не похожим на рассмотренные раньше. Бывают случаи, когда ученики находят такой путь решения, который не предусмотрел сам учитель. Цель, к которой должен стремиться каждый педагог: научить учиться так, чтобы ученик со временем превзошел учителя.
    На внеклассных факультативных занятиях учащиеся получают и домашние задания, в выполнении которых могут принимать участие родители. Кроме того, каждый из школьников может побывать в роли учителя и дома, и в школе. Интересные задачи, решение которых разобрано совместными усилиями учителя и учеников, предлагаются последними родителям. Это важный воспитательный момент — показать ребенку, что он может знать больше и лучше, если поставит себе такую цель.
    Часть факультативных занятий была подготовлена при участии наиболее активных учащихся. Совсем не обязательно сильные в математике ребята могут подобрать интересные задачи, головоломки, забавы с числами, сделать рисунки или выполнить чертеж, таблицу, составить кроссворд. К такой работе привлекаются в той или иной степени все. Наиболее смышленые предлагают головоломные задачи одноклассникам, готовят сообщения или доклады. Тематика этих докладов предусмотрена программой факультативных занятий , а литература для работы подобрана в соответствии с возрастом учащихся.
    В этом году ученики VI класса смогли самостоятельно разобраться в правиле "ложного положения", которое применялось в те времена, когда учился М.В.Ломоносов. Решая подобного рода задачи, шестиклассники удивлялись тому. как сложно было их ровесникам запоминать такие громоздкие правила решения задач.

на предыдущую страницу