Методика разработки
содержания спецкурса
“Прикладная математика”
Некоторые понятия математического моделирования
Слово “модель” ведет свое происхождение от латинского “modelus”, что означает мера, мерило, образец, норма. Термин “модель” широко используется в различных областях человеческой деятельности. Мы будем рассматривать только модели, применяемые в научных исследованиях.
Модель - это такой материально или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что эго непосредственное изучение дает новые знания об объекте-оригинале.
Под моделированием понимается процесс построения, изучения и применения моделей.
Главная особенность моделирования
в том, что это модель выступает как своеобразный инструмент для познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект.Необходимость использования метода моделирования определяется тем, что многие объекты непосредственно исследовать или вовсе невозможно когда объект недосягаем, как, например, Земля и глубины Вселенной и т.п.), или это исследование требует много времени и средств.
Процесс моделирования включает 3 элемента:
1. субъект исследователь;
2. объект исследования;
3. модель, опосредствующую отношения познающего субъекта и познаваемого объекта.
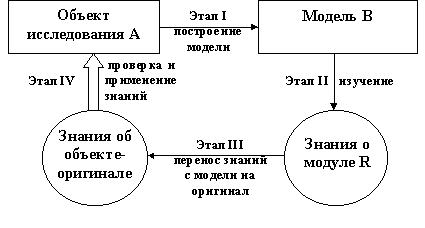
Сущность процесса моделирования схематически отображена на рисунке 1.

Пусть имеется некоторый объект А который необходимо исследовать. Мы конструируем или находим в реальном мире другой объект В - модель объекта А. Этап построения модели предлагает наличие некоторых знаний об объекте-оригинале.
Познавательные возможно эти модели обуславливаются тем, что модель отображает какие-либо существенные черты объекта
-оригинала. Для одного объекта может быть построено насколько “специализированных” моделей.На втором этапе процесса моделирования модель выступает как самостоятельный объект исследования. Конечным результатом этого этапа является множество (совокупность) знаний о модели R.
На третьем этапе осуществляется перенос знаний с модели на оригинал - формирование множества знаний S. Одновременно мы переходим с “языка” модели на “язык” оригинала.
Четвертый этап - практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им. В итоге мы снова возвращаемся к проблематике реального объекта.
Моделирование - циклический процесс. Это означает, что за первым четырехэтапным циклом может последовать второй, третий и т.д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется.
Все множество моделей делится на 2 больших класса: модели материальные (предметные) и модели идеальные (мысленные). Примерами материальных моделей служат фотографии, макет застройки района и т.д. Идеальные модели часто имеют знаковую форму.
Математическое моделирование относится к классу знакового моделирования. При этом модели могут создаваться из любых математических объектов: чисел, функций, уравнений, графиков, графов и т.д.
Создание математической модели - важный этап познания, поскольку он позволяет четко формулировать наши представления о структуре явления, характерных его особенностях, действующих в нем связях.
Для одного и того же явления можно создать не одну, а несколько различных моделей. История науки оставила нам в наследство множество примеров такого рода. Скажем в оптике рассматривались несколько моделей распространения света: корпускулярная, волновая, электромагнитная. Для них были чисто математическим путем выведены многочисленные важные закономерности количественного характера. Каждая из названных моделей требовала особого математического подхода для своего развития и соответствующих специфических математических средств исследования. Так, корпускулярная геометрическая) оптика использовала средства евклидовой геометрии и привела к выводу законов преломления и отражения лучей света.
Волновая модель теории света потребовала новых математических идей - рассмотрение тригонометрических функций.
Одной из самых древних математических моделей, несомненно, является, геометрия Евклида. Это модель окружающего нас пространства и находящихся в нем предметов. Эта модель создавалась на протяжение тысячелетий и несет безотказную службу человеческому знанию в настоящее время, так же как и будет ее нести и в будущем.
Другой древней моделью является абстрактная модель числа предметов, которая появилась в результате счета окружающих нас предметов.
Достаточно широко используются математические модели при анализе экономических проблем. Экономическое моделирование осложняется тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделирование производственных процессов не представляет принципиальных трудностей и не намного сложнее, чем моделирование физических процессов. Моделировать же производственные отношения невозможно, не учитывая поведения людей, их интересов и индивидуальных принятых решений.
Для того, чтобы продемонстрировать различия между моделированием чисто технологических сторон экономических явлений и описанием действий людей, приведем простой пример. Рассмотрим бригаду рабочих с мастером во главе, занятых мелкосерийным производством. Ежедневно перед мастером возникает задача распределения между рабочими заданий на изготовление различных деталей. Рабочие отличаются между собой как по общей квалификации, так и по умению выполнять отдельные производственные операции. Можно математически описать производительность каждого рабочего в каждой операции, выделить операции, необходимые для изготовления каждой детали и оставить задачу о минимальных затратах времени на выполнение полученных заданий. Такая задача сводится к задаче линейного программирования. Однако на практике полученный план распределения вряд ли удовлетворял бы мастера. Дело в том, что операции делятся на “выгодные” и “не выгодные” в смысле их оплаты. Поэтому мастер обязан следить за тем, чтобы все рабочие получили в итоге такую зарплату, которую и сам рабочий, и мастер считали бы “нормальной
”. К сожалению, пока невозможно математически проанализировать эту проблему, поскольку принципы построения математических моделей с учетом экономических интересов отдельных людей и их коллективов разработаны слабо.Нелегкой проблемой в математической экономике является сопоставление теории и практики: экономические показатели измерять крайне трудно - измеряются они все на лабораторных установках, наблюдение удается проводить крайне редко, проводятся они в разных условиях и содержат массу неточностей. Поэтому здесь трудно использовать опыт измерений, накопленный в других науках, к требуется разработка специальных методов.
Вопросы применения математических методов в экономике были разработаны в трудах советского математика Л.В. Канторовича, которые были отмечены Ленинской и Нобелевской премиями.