Нет хороших и плохих методов,
есть хорошее и плохое их применение.

Б.М. Теплов

XI. МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

11.1. ПОДГОТОВКА ПЕРВИЧНЫХ ДАННЫХ К АНАЛИЗУ

    Наблюдая и измеряя характеристики объекта, экспериментатор собирает первичный статистический материал. Дальнейшая задача состоит в такой обработке и представлении первичных данных, которые позволили бы оценить и сопоставить результаты для проверки гипотез, для выявления существенных свойств и закономерностей педагогического процесса. В основе методов обработки лежит предварительное упорядочение, cиcтeмaтиaция первичных данных и вычисление их статистических характеристик.

Обобщенный алгоритм подготовки данных может быть представлен следующим операциями:
    а) все данные формулируются и записываются в необходимой краткой форме;
    б) проводится группировка данных, то есть распределение их на однородные группы в соответствии с интересующими экспериментатора признаками. Данные в каждой группе упорядочиваются - классифицируются, сортируются, структурируются в соответствии с той моделью, которая разрабатывалась при составлении плана-программы (линейный, параллельный или перекрестный эксперимент);
    в) устанавливаются характеристики (признаки, параметры каждой группы данных и производится подсчет абсолютного числа факторов, характеризующих группу (число учащихся, уроков, отметок, ответов и т.д.);
    г) данные внутри каждой сформированной группы располагаются в ряд (вариационный ряд) по убыванию или возрастанию признака. Определяется наибольшее и наименьшее значения признака;
    д) вариационные ряды данных, полученных в номинальной или порядковой шкале, ранжируются. Интервалы группировки по рангам выбираются оптимальными (слишком крупные интервалы скрывают нюансы явлений, слишком дробные - затрудняют o6pаботку). В результате этой операции появляются новые количественные данные;
    е) проводится статистическая обработка полученных количественных данных, заключающаяся в вычислении некоторых статистических характероистик и оценок, позволяющих глубже понять особенности экспериментальных явлений;
    ж) составляются наглядные материалы, отображающие полученную информацию: таблицы, графики, диаграммы, схемы и др., по которым в дальнейшем устанавливаются и анализируются связи между параметрами экспериментальных объектов.

11.2. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЕДАГОГИЧЕСКИХ ОБЪЕКТОВ

    Педагогические явления относятся к числу массовых: они охватывают большие совокупности людей, повторяются из года в год, совершаются непрерывно. Показатели (параметры, результаты) педагогического процесса имеют вероятностный характер: одно и то же педагогическое воздействие может приводить к различным следствиям (случайные события). Тем не менее, при многократном воспроизведении условий определенные следствия появляются чаще других, - это и есть проявление так называемых статистических закономерностей (изучением которых занимаются теория вероятностей и математическая статистика).
    Методы математической статистики в последние десятилетия стали применяться и в педагогике. Поэтому экспериментатору необходимо знание ряда простейших понятий математической статистики и умение с ними работать.
    Все множество интересующих исследователя однородных явлений, событий или их показателей называется генеральной совокупностью данных объектов. Та часть последней, которая подвергается экспериментальному изучению, называется выборочными совокупностью или выборкой.
    Величина (объем) выборки представляет собой абсолютное (счетное) количество однородных объектов исследования (явлений, событий или их характеристик).
    Выборка характеризуется рядом статистических характеристик, наиболее употребительными из которых являются: относительное (процентное) значение, удельное значение, среднее арифметическое значение, дисперсия, среднее квадратичное отклонение среднего арифметического.
    Относительное значение данного показателя - это отношение числа объектов, имеющих этот показатель, к величине выборки. Выражается относительным числом или в процентах (процентное значение).
    Пример: Успеваемость в классе = числу положительных итоговых отметок, деленному на число всех учащихся класса. Умножение этого значения на 100 дает успеваемость в процентах.
    Удельное значение данного признака - это расчетная величина, показывающая количество объектов с данным показателем, которое содержалось бы в условной выборке, состоящей из 10, или 100, 1000 и т. д. объектов.
    Пример: Для сравнения уровня правонарушений в разных регионах берется удельная величина - количество правонарушений на 1000 человек (N)

N = (число правонарушений в регионе)*1000
(население региона)

    Среднее значение данного показателя выборочной совокупности (арифметическое среднее, выборочное среднее) - это отношение суммы всех измеренных значений показателя к величине выборки.

(1)

    Среднее значение недостаточно полно характеризует выборку; за ним скрывается “поведение” самого показателя явления—“разброс”, различное распределение его значений около среднего (так называемая “функция распределения”).
   Пример: Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое - 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.
    Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и среднего квадратичного отклонения.
    Дисперсией (d 2) статистического показателя называется среднее значение квадратов отклонений отдельных его значений от среднего выборочного; дисперсия определяется по формуле:

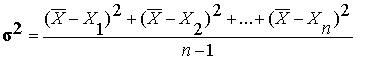(2)

    Средним квадратическим отклонением (экспериментальным) называется корень квадратный из дисперсии.

Image23.gif (1092 bytes) (3)

    Пример: Для предыдущего случая имеем

классы Image24.gif (893 bytes) Image25.gif (855 bytes)
Экспериментальный

контрольный

 19

19

 1

48,5

 1

7

    Это означает, что в одном классе посещаемость высокая, стабильная, а 1 другом - отличается непостоянством.
    Дисперсия и среднее квадратичное отклонение играют большую роль при определении степени достоверности результатов.
    Генеральная совокупность также обладает всеми вышеперечисленными статистическими характеристиками, которые в общем случае не совпадают с характеристиками выборки. Для эксперимента особое значение, имеет оценка той ошибки, которая допускается, если по выборочным характеристикам судить о генеральной совокупности.
    В практике вычислений величина расхождения средних значений генеральной и выборочной совокупностей определяется средней квадратической ошибкой выборочного среднего, которая вычисляется по формуле

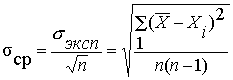
Image22.gif (1632 bytes)

11.3. СОДЕРЖАТЕЛЬНЫЙ АНАЛИЗ ДАННЫХ И ПОЛУЧЕНИЕ ВЫВОДОВ

    Общий алгоритм содержательного анализа данных эксперимента был приведен в гл. VI. Основными задачами анализа являются сравнение полученных данных по тем схемам, которые были заложены в логику исследования, установление справедливости гипотез, определение степени достижения целей и задач эксперимента.
    Но не менее важной задачей является объяснение внутренних причин получившихся результатов, психологическая интерпретация педагогических выводов. Л. В.3анков предостерегал исследователей от установления лишь поверхностных, эмпирических связей типа: учитель действовал так-то — получилось то-то; учитель действовал иначе — получилось другое. Такой анализ, не дающий объяснения эффективности педагогических воздействий, обедняет выводы, сужает область их применения. Поэтому следует обсудить весь комплекс количественных и качественных показателей, измерений и наблюдений педагогического процесса, на основе чего открывается возможность объяснить результаты и перейти к формулированию выводов.
    Важнейшим условием такого всестороннего и глубокого анализа является квалификация экспериментатора, его способность к анализу и осмыслению — обобщению фактов. Экспериментатору следует также предостеречься от опасности субъективизма в интерпретации данных, подгонки данных к имеющейся гипотезе. Ведь результаты эксперимента обрабатываются теми, кто его проводит, и это накладывает на экспериментатора и руководителя особую ответственность.
    Большую роль играет владение некоторыми специальными способами предоставления полученных данных в наглядной — краткой и схематизированной—форме. Информация, сконцентрированная на одной небольшой площади, позволяет одновременно воспринимать различные по содержанию сведения в их сравнении.
    Табличный способ изображения данных позволяет представить подробные количественные данные с кратким сопроводительным объясняющим текстом. Таким текстом служат название таблицы, раскрывающее связь между числовыми рядами, и внутренние заголовки таблицы (указывающие измеряемые признаки, место, время, единицы измерения и т. п.).
    Матрица представляет собой разновидность таблицы со строками и рядами, имеющими какие-либо функционально-логические связи. При составлении матрицы связи или их отсутствие отмечаются в клетках условными знаками. Результирующий вид матрицы обнаруживает наличие связей между различными факторам педагогического процесса.
    Графики еще более наглядно, чем таблицы, отображают изменение экспериментальных данных. Графики—полигоны строятся в прямоугольной системе координат, в которой на оси “X” отмечается значение независимой переменной (время, место, категория и др.), а по оси “Y” — значение или порядок признака.
    Гистограмма представляет собой разновидность графика в котором по оси “Y” откладываются интервальные (дискретные значения какой-либо группировки, в результате чего график становится “ступенчатым”.
    Диаграммы сопоставляют количественную информацию в виде площадей различных фигур (круг, прямоугольник и др.).
    Графы — особый вид графического отображения данных результатов; это фигура, состоящая из точек — вершин, соединенных отрезками-ребрами. Вершины графа могут обозначать различные компоненты педагогического процесса, параметры, факторы, а ребра — отношения и связи между ними. Графы (как модели) часто применяются на этапе прогнозирования эксперимента, а на обобщающем этапе с ними сопоставляются результаты. Простейшим примером графа служит “дерево” целей.

11.4. ДОСТОВЕРНОСТЬ РЕЗУЛЬТАТОВ

    Как уже отмечалось, основным свойством педагогических процессов, явлений является их вероятностный характер (при данных условиях они могут произойти, реализоваться, но могут и не произойти). Для таких явлений существенную роль играет понятие вероятности.
    Вероятность (Р) означает степень возможности осуществления данного события, явления, результата. Вероятность невозможного события равна нулю, достоверного — единице (100%). Вероятность любого события лежит в пределах

    Если в эксперименте получен какой-то количественный результат (X), то возникает вопрос: какова вероятность того, что этот результат будет получен в повторном эксперименте при тех же условиях.
    Математическая статистика отвечает на этот вопрос так: вероятность точного повторения результата приближается к нулю.
    Но, если задать некоторую область значений результата (так называемый доверительный интервал

 ХДОВ), то можно говорить об определенной вероятности того, что результат повторного эксперимента будет находиться в пределах этой области.
    Достоверностью (надежностью, значимостью) Р среднего результата серии педагогических измерений будем называть вероятность того, что среднее значение измеряемого параметра при повторном эксперименте попадает в данный доверительный интервал.
    Итак, результат серии педагогических измерений должен быть выражен средним арифметическим с указанием доверительного интервала и достоверности.ДОВ (с достоверностью=Р) (5)

    В этой формуле заключается статистический смысл принципа воспроизводимости педагогического эксперимента: если повторить (или дублировать) эксперимент, то его результат будет с определенной вероятностью находиться в пределах доверительного интервала Image28.gif (980 bytes).
    В строгом научном эксперименте принято добиваться не менее, чем 95%-ной достоверности, хотя в ряде случаев (например, в разведывательном эксперименте) оправдан и 50%-ный уровень.
    Определение доверительного интервала. Между числом измерений, величиной доверительного интервала и достоверностью существует определенная зависимость. Для малых по объему выборок (что чаще всего и имеет место в педагогическом эксперименте) эта зависимость исследована английским математиком Стьюдентом (Госсетом) и отображена в таблице 1.

Таблица 1. Коэффициент Стьюдента

n/p 0,8 0,9 0,95 0,98 0,99
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
? 		3,08
1,89
1,64
1,53
1,48
1,44
1,42
1,40
1,38
1,37
l,363
1,36
1,35
1,35
1,34
1,34
1.33
1,33
1,33
1,38
1,32
1,32
1,32
1,32
1,32
1,32
1,31
1,31
1,31
1,30
1,30
1,29
1,28		 6,31
2,92
2,35
2,13
2,02
1,94
1,90
1.86
1,83
1,81
1,80
1,78
1,77
1,76
1,75
1,75
1,74
1,73
1,73
1,73
1,72
1,72
1,71
1,71
1,71
1,71
1,70
1,70
1,69
1,68
1,67
1.66
1,65		 12,71
4,30
3.18
2,77
2,57
2,45
2,36
2,31
2,26
2.23
2,20
2,18
2,16
2,14
2,13
2,12
2,11
2,10
2,09
2,09
2,08
2,07
2,07
2.06
2,06
2,06
2,05
2,05
2,05
2,02
2,00
1,98
1,96		 31,8
6,96
4,54
3,75
3,36
3.14
3,00
2,90
2,82
2,76
2,72
2,68
2,65
2,62
2,60
2,58
2,57
2,55
2,54
2,53
2,52
2,51
2,50
2,49
2,49
2,48
2,47
2,47
2,46
2,42
2,39
2,36
2,33		 63,7
9,92
5,84
4,60
4,03
4,71
3,50
3,36
3,25
3,17
3,11
3,06
3,01
2,98
2,95,
2,92
2,90
2,88
2,86
2,85
2,83
2,82
2,81
2,80
2,79
2,78
2,77
2,76
2,76
2,70
2,66
2,62
2,58

    Для определения доверительного интервала по методу Стьюдента-Госсета:
    а) по формуле [1] рассчитывают среднее арифметическое значение параметра —Image4.gif (866 bytes) ;
    б) по формуле [4] рассчитывают среднюю квадратичную ошибку среднего —
    в) задаются необходимой величиной достоверности Р;
    г) по известному числу расчетных данных (количеству объектов) и требуемой достоверности входят в таблицу 1 и определяют коэффициент Стьюдента — Image29.gif (848 bytes) ;
    д) доверительный интервал определится так

Image81.gif (1042 bytes) (с достоверностью=Р)

    Результат экспериментальной серии n изменений в методике Стьюдента выражается так

Image31.gif (1009 bytes)

    Пример. Рассчитать результат (средней балл и доверительный интервал) срезовой контрольной работы в экспериментальном классе. Всего учащихся — 30 человек, из них получили оценки: “5” — 6 человек; “4” — 10; “3” — 12; “2” — 2 человека.
    Расчет
    а) Средний балл Х =

    б) Средняя квадратичная ошибка среднего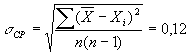

Image32.gif (1371 bytes)

    в—г) Задаемся 95%. достоверностью и по таблице 1 находим

Image33.gif (941 bytes)

    д) Вычисляем доверительный интервал;

Image34.gif (1225 bytes)

    Результат контрольной работы

Image35.gif (1225 bytes)

    Значит, результат аналогичной повторной контрольной работы в этом классе будет с 95% вероятностью лежать в этой области (от 3,5 балла до 3,9 балла).

    Достоверность сравнения. Средние значения параметров педагогического процесса, полученные в результате срезовых измерений в различных группах (экспериментальной и контрольной) могут быть близкими, но никогда не бывают одинаковыми ( и ). Вывод же о справедливости гипотезы может быть сделан на основании заключения либо о различии, либо о сходстве результатов.
    Для того, чтобы определить, является ли разность между и существенной (статистически достоверной) выполняются следующие операции:
    а) для обеих групп объектов задается одинаковый уровень достоверности (к примеру Р=0,9);
    б) вычисляются средние арифметические значения для групп и ;
    в) вычисляются средние квадратичные ошибки средних значений Image36.gif (976 bytes);
    г) по таблице для каждой группы определяется коэффициент Стьюдента Image29.gif (848 bytes) ;
    д) определяются доверительные интервалы;

Image82.gif (1251 bytes)

    е) вычисляется разность -;
    Если окажется, что

Image83.gif (1169 bytes)

    то разница между показателями должна считаться существенной с достоверностью Р == 0,9.
    Если окажется, что

Image84.gif (1165 bytes)

   то должно считаться существенным сходство между результатами обеих групп.
   Если окажется, что

Image85.gif (1156 bytes)

    то следует

    При этом экспериментатор должен помнить, что cущecтвoвание значимой разницы или сходства количественных показателей без поддержки другими аргументами нельзя брать в основу выводов (особенно в сомнительных случаях).
    Правомерность применения статистик. Статистические показатели, получаемые на основе номинальных и порядковых измерений, предоставляют экспериментатору богатый аналитический материал, однако их следует использовать весьма осторожно и обязательно вместе с материалом, полученным из других источников. Статистические характеристики предназначены прежде всего для обработки измерений, выраженных в интервальной шкале. Операции же с номинальными и порядковыми показателями осуществляются условно (с определенной степенью огрубления) и допустимы лишь в рамках межгруппового сравнения.
    В частности, в педагогической литературе существует различное мнение о возможности применения методов математической статистики к данным школьной пятибалльной системы оценок. То обстоятельство, что эти отметки - всего лишь ранговые величины, которые следует считать субъективной порядков оценкой, а не точным интервальным измерением, делает несостоятельными в применении к ним методы параметрического статистического анализа.
    Примечание. Если говорить о субъективизме, то в других, считающихся гораздо более объективными, методах измерения психолого-педагогических характеристик (к примеру, подсчет количества ошибок, действий, реакций, времен, сил и т. п.) субъективный фактор присутствует не в меньшей степени, чем в балльной оценке.
    Рекомендация. В практике нестрогого экспериментирования целесообразно данные статистического анализа использовать для выработки решений и выводов наряду с разнообразными качественными характеристиками педагогического процесса и другими материалами.

Рекомендуемая литература

    Аванесов В. С. Применение статистических методов и ЭВМ в педагогических исследованиях. // Введение в научное исследование по педагогике. / Под. ред. В. И. Журавылева. М., 1988*.
    Грабарь М. Н. и др. Применение математической статистики в педагогических исследованиях. М., 1977.
    Журавлев В. И. Обработка и интерпретация научных данных в педагогическом исследовании. // Введение в научное исследование по педагогике. / Под ред. В. И. Журавлева. М., 1988*.
    Занков Л. В. О предмете и методах дидактических исследований, М., 1962.
    Кабанова-Меллер Е. Н. Проблема эмпирического и теоретического обобщения в советской педагогической психологии. // Сов. педагогика.—1973 — № 11*.
    Как провести социологическое исследование. // Под ред. М. К. Горшкова и др.—М.:— 1985. С. 143—164.
    Кыверляг А. А. Условия эффективности и достоверности научного исследования. // Сов. педагогика. — 1988. — № 5*.
    О моделировании педагогических явлений. // Новикова Л. И. и др. Путь к творчеству. М., 1966, с.110-120.
    Павлов Ю. В. Статистическая обработка дидактического эксперимента. М., Знание, 1977.
    Полонский В. М. Критерии теоретической и практической значимости исследований. // Сов. педагогика. — 1988. — № 11*.
    Полонский В. М. Оценка качества научно-педагогических исследований. М., 1987*.
    Штульман Э. А. Специфика методического эксперимента, // Сов. педагогика. — 1988. — № 3*.

Дополнительная литература

    Архангельский С. И. Лекции по научной организации учебного процесса в высшей школе. М., 1976, с. 148-168.
    Битинас Б. П. Многомерный анализ в педагогике. М., 1971,.
    Гласс Д. и др. Статистические методы в педагогике и психологии. М., 1976.
    Колкот Э. Проверка значимости. М., 1978.
    Паповян С. С. Математические методы в социальной психологии. М., 1983.
    Рабочая книга социолога. М., 1983.
    Селевко Г. К. Обработка результатов измерений. // Лабораторный практикум по курсу общей физики. Ярославль, 1976*.
    Сокольников Ю. П. Системный анализ. М., 1986*.
    Социальная психология. // Под ред. А. В. Петровского. М., 1987*.
    Фридман Л. М. О корректном применении статистических методов в психолого-педагогических исследованиях. // Сов. педагогика. — 1970.—№ 2*.
    Черепанов В. С. Экспертные оценки. М., 1989*.