§ 8. Методика преподавания курса

Курс “Закономерности окружающего мира” - один из интегративных предметов педагогического эксперимента “Экология и диалектика”, поэтому он не является только курсом теории вероятностей для школьников. Цель предмета шире, нежели просто ознакомление учащихся с еще одной, незнакомой доселе, областью математики, а развитие, вследствие углубления и расширения математического кругозора, интеллектуального и творческого потенциала подростков.

Название эксперимента - “Экология и диалектика” - отражает самое главное в существовании человека: его умение жить в гармонии с окружающим миром - природой, людьми, обществом, способность к постоянной адаптации, смене стиля жизни и мышления с тем, чтобы “вписаться” в столь быстро меняющийся мир.

Целью эксперимента является раннее и разностороннее развитие детей, формирование их экологического и вероятностного мышления. Это является и целью преподавания ЗОМ. Жизнь постоянно ставит нас перед необходимостью выбора, и школа должна научить детей анализировать ситуацию, просчитывать возможные результаты и, как следствие, принимать в данной ситуации оптимальное или близкое к оптимальному решение.

Преподавание курса ЗОМ велось практически без учебных пособий, что определило единственно приемлемую в данных условиях методику преподавания: проблемное обучение, соавторство учителя и ученического коллектива в создании и реализации урока.

Изучение ЗОМ строилось так, чтобы явить собой для учащихся продолжительный по времени исследовательский процесс, затрагивающий разнообразные и часто незнакомые области человеческого существования, поиск ответов на возникающие в процессе этого исследования, вопросы, выдвижение различных гипотез, их рассмотрение и выбор наиболее достоверных из них, анализ отобранных, их оценка и - возможно -получение закономерного результата.

Тема первая: “Хаос и Порядок

Первая тема курса “Хаос и Порядок” предлагает учащимся проблемы глубокого философского плана, воспитывает в детях планетарное сознание. Ребенок становится на позиции вдумчивого исследователя Мира, бесконечно радуется и удивляется результатам своего исследования, делает неожиданные для себя выводы, учится по-новому воспринимать окружающую его действительность.

Что есть Хаос? Неразделенность верха и низа, черного и белого, холода и тепла, дня и ночи. Хаос есть жуткая смесь всех стихий. Трудно представить себе мир сплошного Хаоса, но шестиклассники отправляются туда в “путешествие”, откуда привозят небольшие “путевые заметки” и “репортажи” (результаты домашних работ).

“Пришло время завтрака. Я решила сварить кашу и поставила кастрюлю с грибами на огонь. Когда вода превратилась в лед, я добавила побольше соли, ведь компот должен быть очень-очень сладким. Потом крикнула ребятам: “Эй, пирог уже прокис, идите сюда!”(Наташа 3.)

“Красивое дерево стояло передо мной. Потом оно резко щелкнуло, и его верхняя часть превратилась в огромный цветок с чудесным запахом. Цветок опустил свои лепестки к земле, и они превратились в толстых змей, сросшихся хвостами. Змеи, шипя, свились в клубок, сжались и сорвались вниз. Едва они коснулись земли, как сразу превратились в старый грузовик. Он проехал 20 метров и взорвался”. (Дима Л.)

Человеку неуютно в царстве Хаоса. Людям свойственно стремиться к гармонии, порядку. Примером создания из Хаоса Порядка служит мифотворчество.

“Вначале Эвринома, богиня всего сущего, восстала из Хаоса и обнаружила, что ей не на что опереться. Поэтому она отделила небо от моря и начала свой одинокий танец по волнам...”. (пеласгический миф творения)

“Чернокрылая Ночь ответила на ухаживания Ветра и снесло во чрево темноты серебряное яйцо. Из этого яйца был высижен Эрос, который и   привел Вселенную в движение...”. (орфический миф)

“Вначале всех вещей из Хаоса возникла мать-Земля и во сне родила сына Урана. Высоты горных вершин пролил Уран на спящую мать животворящий дождь, и она породила травы, цветы и деревья, зверей и птиц...”. (олимпийский миф)

Полные поэзии, мифы Творения настраивают детей на особый лад. Обыденность привычного уходит, отодвигается, позволяет осознать Чудо - существование нашего Мира. И осуществляется переход в сознании - дети понимают - этот Мир надо любить и беречь.

Надо заметить, что попытки собственного мифотворчества дали довольно скромные результаты в первой группе шестиклассников. Поэтому' в дальнейшем детям предлагалось или создать какой-либо миф самим (необязательно о сотворении Мира), или найти интересный миф в литературе.

Хаос постоянно врывается в нашу жизнь. Учащиеся в качестве домашней работы должны были коснуться следующих вопросов: каковы могут быть проявления Хаоса в нашей Жизни, всегда ли Хаос - зло, какие способы борьбы с Хаосом использует человек?

“Я вернулась с уроков и увидела, что цветы в вазе завяли. Я их вынула, обмыла и подрезала стебли, сменила воду. Цветы ожили, сразу стало красиво”. (Женя Р.)

“Утром все очень спешили. Домой я вернулась первой. Вымыла грязную посуду, прибрала, подмыла полы. Всем будет приятно видеть наш дом чистым”. (Ира М.)

“Детальки валялись как попало на моем столе. А я - хлоп - хлоп - и сделал из них робота”.
(Саша Д.)

“Я проболела и долго не была в лесу. Когда пришла, увидела, что на поляне больше нет берез - одни пеньки кругом. И я заплакала”.(Люба К.)

“У меня мысли вертятся, путаются. А когда я возьму чистый лист и краски, все становится так ясно, и получается новый рисунок”.(Лена П.)

Стремление человека к Порядку богато представлено и русским фольклором - различными приметами, пословицами, поговорками. Не обходим стороной и суеверия. Аукцион примет, пословиц и поговорок проходит очень живо, ребята проделывают большую поисковую работу, готовясь к нему.

Моделирование мира, где царит абсолютный Порядок, предоставляет шестиклассникам еще одну возможность проявить себя. Они строят свой мир, безусловно, фрагментарный, и в этом мире устанавливают свой собственный порядок вещей и явлений.

"Правила на каждое утро.

1. Встать в 6 часов.
2. Вывести погулять собаку.
3. Вернуться, покормить собаку, сделать зарядку.
4. Приготовить и съесть завтрак.
5. Привести себя в порядок и в 7.30 отправиться в школу (или на работу)"(Вика Л.)

Миры обсуждаются в классе.

- Вика, у меня собаки нет!
- Иди гулять с поводком.
- А можно взять игрушечную собачку?
- Можно.
- Вика, а если воскресенье или праздник, все равно вставать так рано?
- Никаких праздников!
- Вика, а как же каникулы?
-Каникулы вообще отменяются!
- Ничего себе придумала!!!

“Я утверждаю расписание дня и погоды на Земле.

0.00 - 4.00. Ночь. Плотная облачность, сильный дождь. Ветра нет.
4.00 - 7.00. Утро. Легкий ветерок. Облачно без дождя.
7.00 - 12.00. День. Ясно, очень тепло и солнечно.
12.00-14.00. Тепло. Облачно без дождя.
14.00 - 18.00. Очень солнечно, жарко.
18.00 - 20.00. Вечер. Облачно, небольшой дождь.
20.00- 0.00. Ночь. Облачно. Очень сильный ветер, почти ураган”.(Рома Б.)

- Рома, так я, получается, и звезд никогда не увижу?
- Ну, не увидишь! Зато зонтика не надо - дождь строго по расписанию.

Множество моделей предлагается ребятами. Миры получаются разными в зависимости от личности ребенка, проявления его внутреннего “я” (в одних мирах царит стремление к гармонии, в других преобладают идеи потребительства, третьи полны агрессии и деконструктивных идей). Обсуждение моделей позволяет учащимся сделать вывод) что абсолютный Порядок лишает нас возможности удивляться, обедняет мысли и чувства, ограничивает свободу и творчество (в мире Хаоса последнее и вовсе невозможно).

Большое значение в изучении первой темы имеют игры. Как может проявить себя Случай? Это хорошо видно в игре “Мудрый попугай”. Играем всем классом. В качестве домашней работы ребята заготавливают карточки двух типов: на одних записываются вопросы, на других - ответы (желательно в обтекаемой форме, без излишней конкретизации). В классе все вопросы и ответы раскладываются по двум коробкам. Учащиеся выбирают среди товарищей “попугая”, и “мудрая птица” с коробкой ответов занимает место у доски. Остальные участники игры будут задавать “попугаю” вопросы (коробка с карточками-вопросами передается по ряду, ребята извлекают наудачу карточку и читают вопрос). “Попугай”, вынимая наугад карточку из своей коробки, выдает громким голосом ответ, выказывая свою безусловную мудрость. Иногда получается полная бессмыслица, иногда - нечто осмысленное.

“- Хочешь побывать на Гаваях?
- Мне мама не разрешает”.

“- Что бы ты хотел получить в подарок?
- Сахарную косточку”.

“- Вы мечтаете стать президентом?
- Стоило бы попробовать”.

“- Почему Круз и Иден все время ссорятся?
- Трудно выбрать между “Баунти” и “Сникерсом”.

Игра происходит очень живо. Случайным образом выбранные фразы могут нести осмысленную информацию, и это увлекает детей.

Игра “Лаборатория слова” состоит в следующем. Дети заготавливают карточки, на которых записывают отдельные буквы или слоги. В классе все эти заготовки складывают в большую коробку. Взятые наугад карточки крепим на доску, и, рано или поздно, рождается Слово. Его встречают радостно: “Ура!”, “Есть!”, “Вижу!”.

Творческая работа по “генерированию” случайных образов проводится без предварительной подготовки. Во время урока на доске записываются несколько предложенных ребятами существительных. Например: Лампа, Конь, Куст. К ним подбираются подходящие по смыслу прилагательные. Все это записывается в следующем виде:

Лампа красивая стеклянный китайская настольная разбитая

Конь вороной быстрый легконогий золотогривый дикий

Куст густой увядший колючий душистый сломанный

Предлагаю ребятам выбрать прилагательные, которые к данному существительному, на их взгляд, наиболее подходят. Выбираются, например, прилагательные стеклянная (лампа), золотогривый (конь), увядший (куст). Все готово к “генерации” образов: первый вариант получает задание нарисовать стеклянный куст, второй - золотогривую лампу, третий - увядшего коня.

После первой “генерации”, рассмотрев и обсудив наиболее удачные работы, приступают ко второй. От первой она отличается другим набором образов и тем, что нет ограничения в выборе “генерируемого” образа. Условия работы можно варьировать.

Завершающим по смыслу в первой теме является урок “Мир Уникальных Людей”. Мы рисуем на доске и в тетради Дерево Жизни:

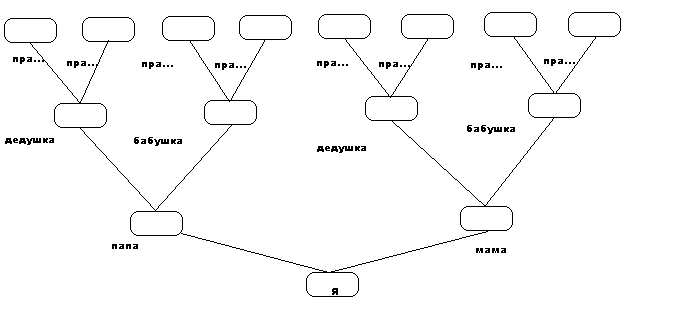
Основа одна, но каждый “делает” Дерево Жизни своим: “Я, Алена”, “Мама Вера”, “Дед Игнатий Петрович”. Редко удается пробраться дальше прадедушек и прабабушек. Не обходится и без курьезов: ребята часто не знают отчеств дедушек и бабушек, а иногда даже и родителей. Но вот необходимая работа проделана, Дерево Жизни построено. В памяти каждой семьи живут истории, когда Случай так или иначе повлиял на ее жизнь. “Прадеда Степана в 1-ю мировую немцы повели на расстрел. Шли по берету крутому, он смотрит - в воду глубоко дерево съехало, только макушка торчит. Он и махнул вниз. Под водой за ствол уцепился, и держится, чтоб не всплыть. Немцы постреляли-постреляли в воду и ушли. А дед потом выплыл”.

Историй много, во всех случай или уберег прародителей от гибели, или случайно свел их в семейные пары, или ... А результат? Дети открывают для себя удивительный факт: если бы в тот давний момент Случай распорядился иначе, их - сегодняшних учеников шестого класса - на свете не было. Совсем! То есть само появление их на свет, обусловленное, вообще говоря, цепочкой случайных событий, есть явление уникальное. Следовательно, каждый из них - Уникальный Человек! Дети ошарашены своим открытием, им необходимо время, чтобы осознать себя проявлением Чуда.

Ранее ребята услышали о Великом Чуде - нашей планете. Оказалось, Чудесная планета населена Чудесными людьми (и это, по логике вещей, закономерно). Когда первое потрясение проходит, шестиклассникам предстоит пережить другое, куда более сложное и несравненно более ценное в плане самовоспитания: если отступить с позиции “я”, сделанное открытие видится в свете ином - любой существующий рядом с тобой человек уникален, каждый человек есть проявление Чуда.

Стоит провести такой урок хоть раз, чтобы увидеть по завершении разговора серьезные лица ребят и особое выражение их глаз.

Я ставлю вопрос: как должны строить свои отношения живущие на Уникальной Планете в мире Уникальных Людей? Задание на дом - творческая работа “Правила для Уникального Человека”. Результаты работы будут интересными, мы обсудим их в классе.

“Не должно быть насилия”. (Юра О.)
“Не должны такие люди пить вино”. (Леня X.)
“Нельзя лишать своих детей надежды”. (Света П.)
“Уникальным людям никто и ничто не мешает”. (Стас Г.)
“Старайтесь убивать меньше животных, чтобы они совсем не исчезли”. (Дима Л.)
“Надо обязательно передавать свои знания другим”. (Лена С.)
“Взрослые так должны любить своего ребенка, чтобы он чувствовал, что его любят и знал, что он не один”. (Аня С.)
“Охраняйте природу, берегите”. (Олег Ч.)
“Люди не должны убивать друг друга”. (Катя И.)
“Если один человек что-то делает, а у него не получается, не надо стоять и смотреть, а просто надо помочь!” (Маша С.)
“Будьте милостивы”. (Лена К.)
“Растет в пустыне цветок. Не рви его, оставь - пусть растет, ведь он единственный”. (Вова Ч.)
“Люди должны беречь друг друга и любить”. (Алеша С.)

Конечно, результаты творчества различны, как различны и сами дети. Но большая внутренняя работа очевидна, ребята поднимаются на новую ступень в своем развитии, их самосознание претерпевает серьезное изменение.

Последний урок темы “Случай - это серьезно”. Мы посвящаем его литературе - читаем в классе и обсуждаем рассказ Р. Бредбери “И грянул гром”.

Тема вторая: “Множества”

Изучение темы начинается с повторения, так как основные понятия теории множеств учащимся уже знакомы (изучение курса математики в 5-м классе в рамках эксперимента начинается именно с темы “Множества и операции над ними”). Повторение начинаем в форме игры (игра называется “Контакт”, она формирует у младших школьников осознанное отношение к термину “Множество”). Далее можно повторить операции над множествами (быть может, воспользовавшись веревочками Т. Варги). Новым в теме “Множества” является понятие меры. Начинаем с конечных множеств. Моделируем вместе с ребятами шкалу признаков (характеристик), которые могут быть использованы при сравнении свойств пары вещественных объектов, например карандаша и блокнота. В этой будут упомянуты и цвет, и форма объекта, функциональное назначение предмета и даже его запах (оказывается, блокнот пахнет пылью), однако рано или поздно появится нужное слово “вес”. Остановимся на этой характеристике, поговорим о ней подробнее, рассмотрим различные примеры и убедимся, что вес - надежная, скорее даже универсальная характеристика материального объекта. Найдутся - по аналогии - и другие универсальные характеристики: длинна, объем, площадь.

С уровня материального перейдем к абстрактному: перед учащимися ставится вопрос - существует ли подобная универсальная характеристика для множеств? Ответ не заставит себя долго ждать, кто-нибудь из ребят догадается, что такой характеристикой может служить количество элементов различных множеств. Примеры, подтверждающие догадку, разнообразны: “Множество девочек с именем Ира у нас больше, чем множество с именем Лена” (в классе три Иры и две Лены);

“Множество уроков во вторник больше множества уроков в четверг”; “Множество жвачек в моем кармане больше, чем у Антона - он свои уже съел!”.

Итак, вводим понятие меры конечного множества, вводим обозначения и учимся писать фразы типа:

А= {0;*; „ ; а; 2}, m(А)=5 (или 1 А1 =5)

(почему-то запись с буквой “m ” нравится детям больше).
После чего, в качестве устного закрепления, учащиеся придумывают друг для друга вопросы:

“Какова мера множества жен Синей Бороды?”
“А мера множества кроликов, носящих очки?” (Буря споров. Стандартный ответ - ноль. Автор, однако, утверждает, что два: один кролик из “Винни-Пуха”, другой - из “Алисы в стране чудес”). Самое сложное и, следовательно, самое интересное - впереди.

Что делать, если количество элементов множества сосчитать невозможно? Обязательно прозвучит ответ: “У таких множеств меры нет!”, Это скажет кто-нибудь из торопливых. Неторопливые хорошо помнят об универсальности характеристики “мера”. Вопрос конкретизирую: рассмотрим два отрезка. Обозначим за А множество точек первого отрезка, за В - множество точек второго отрезка. Эти множества конечны или бесконечны? Какую численную характеристику можно ввести для сравнения этих множеств? И сразу два открытия, одно за другим:

• Оба множества бесконечны (а длины отрезков различны)!
• Сравнивать можно длину соответствующих отрезков!

Задачу усложняю. Теперь рассмотрим множество точек, лежащих внутри прямоугольников.

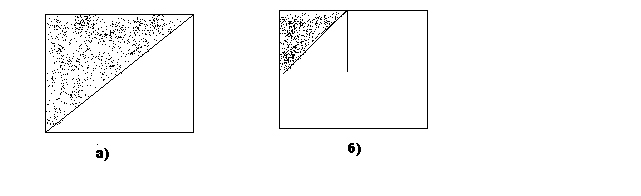
Что может служить мерой этих множеств? Ребята моментально выдают ответ: в этом случае мерой бесконечных множеств может служить площадь прямоугольников.

Домашнее задание состоит в изготовлении мини-тренажера - карточки с тремя графически заданными множествами для определения меры множеств и их подмножеств. Такими карточками ребята обменяются в начале следующего урока с тем, чтобы проверить результаты работы друг друга и оценить их.

Изучение пункта “Отношение мер множества и его подмножества” служит пропедевтикой элементарных вероятностных задач. Опорой в формировании соответствующего навыка служат малые (ученические) и большой (учительский) тренажер с изображенными множествами и подмножествами.

Тема третья: “Введение в комбинаторику”

Существование комбинаторики как раздела математики является для ребят большим открытием, однако само слово “комбинаторика” - такое звонкое и рычащее - поначалу их пугает. И первый пробный шажок в Стране комбинаторике приходится делать очень осторожно. Мы приступаем к моделированию комбинаций с заданными свойствами, решая задачу про зубного врача. Накануне дома учащиеся заготавливают вспомогательный материал из цветной бумаги: 5 групп геометрических фигурок разного цвета (внутри группы, состоящей из 10-ти элементов, форма и цвет фигурок едины), и раскладывают его в конверты. “Ира, Стаc и Олег отправились к зубному врачу. Сколькими способами они могут составить очередь перед кабинетом?”.

Чтобы ответить на поставленный вопрос, учащиеся приступают к моделированию вариантов с помощью вспомогательного материала. Готовые наборы ребята выкладывают на краю парты. По окончании работы совместно обсуждаем результат, ребята производят взаимопроверку. Процесс моделирования их увлекает, и ребята предлагают: “Давайте еще такие задачи решать, только пусть ребят будет больше”. Продолжаем урок, итак “Ира, Стаc, Олег и Женя отправились к зубному врачу...”.

Когда навык решения задач такого типа освоен, переходим на более высокий уровень - моделирование с помощью деревьев. С понятием “дерево” наши шестиклассники познакомились еще в пятом классе. В курсе математики разложение натуральных чисел на множители осуществляется именно “деревом”, способ разложения “в столбик” рассматривается как альтернативный. Например, разложение числа 210 выглядит так: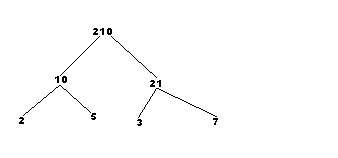

Поэтому учащиеся достаточно быстро овладевают навыком моделирования выборок “деревом”:

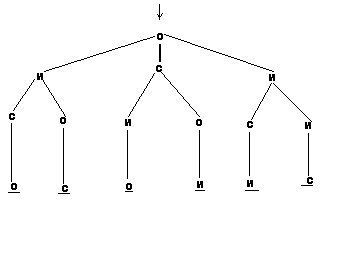
в первом случае, и во втором

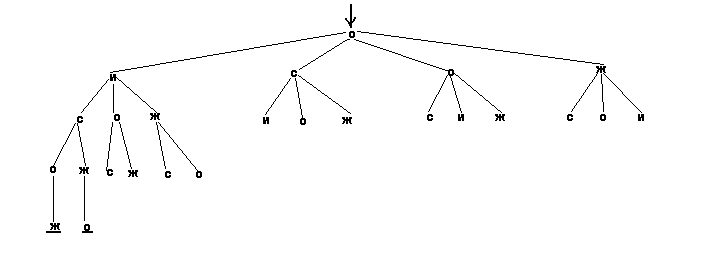
Когда отработан и этот навык, перед учащимися ставится проблема: хорошо было бы найти единое универсальное правило, позволяющее решать задачи такого типа без моделирования; для этого необходимо уловить некоторую закономерность между условием задачи и ее ответом (практический багаж к этому времени накоплен уже приличный и не сводится к одной задаче про зубного врача). Некоторое время дети работают над проблемой самостоятельно, очень сосредоточенно и серьезно, потом тишина сменяется рабочим полушепотом - ребята спонтанно переходят к групповой форме работы, затем и группы становятся тесны - начинается активный обмен мыслями между группами, и в определенный момент “всплывает" - таки пойманная закономерность. Поскольку ничего на веру не принимается, все уже решенные задачи просматриваются вновь, решаются с применением открытого правила, ответы сравниваются, и шестиклассники довольно гудят: “Годится!”.

Тогда я предлагаю на рассмотрение учащихся формулу Рп= п! Как правило, эта формула и слово “факториал” действует на детей, как некоторый эмоциональный допинг: они возбуждаются, “взахлеб” решают простейшие примеры на закрепление понятия “факториал” (например, 6! -4! =), требуют новых примеров и звонок на перемену встречают недовольным “Ну-у-у!”. Есть, очевидно, в этом слове “факториал” и в этом знаке - п! - некоторая скрытая магическая сила (очередное проявление Чуда? Проявление гармонии? Или просто открытие новых возможностей?). В качестве задания для домашней работы учащимся предлагают вычислительные примеры, содержащие знак факториала, которые сводятся к выполнению арифметических действий с обыкновенными дробями.

Следующий за “открытием” формулы урок посвящается решению разнообразных задач. Метод решения - любой: моделирование - предметное или с помощью дерева, или использование формул. Домашнее задание будет творческим: учащиеся придумывают собственные задачи, оформляют их на листочках или в форме книжечки и обязательно решают. Авторские эти задачи будут затем рассматриваться на уроке, включаться в самостоятельные работы, из них будут составляться тренажерные листы задач.

По такой же схеме: предметное моделирование - графическое моделирование - введение формулы шестиклассники учатся решать задачи на сочетания. Стартовой служит задача про магазин “Все для чая”. В оригинале (6) она звучит так:

“В магазине “Все для чая” есть 5 различных чашек и 2 разных блюдца. Сколькими способами можно купить чашку с блюдцем?” Мы начинаем с упрощенного варианта задачи: есть 3 чашки и 2 блюдца. Чтобы ответить на поставленный вопрос, ребята приступают к моделированию чайной пары (пока на предметной основе, в роли чашек и блюдец выступают разноцветные бумажные фигурки). Варьируем условие задачи, решаем аналогичные, добиваясь того, чтобы моделирование производилось без больших затруднений. Потом учимся моделировать с помощью деревьев:

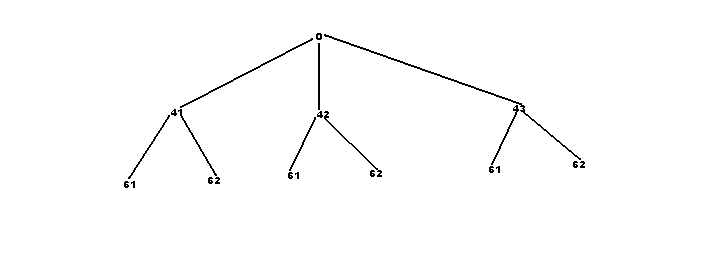
Затем вводится формула для подсчета числа сочетаний. Ребята также составляют авторские задачи.

При решении задачного материала (предложенных учителем или авторских, при выполнении домашней или классной работы, в процессе взаимоконтроля) способ решения строго не оговаривается, и учащиеся могут воспользоваться тем приемом, которым владеют в большей мере (моделированием или с помощью формул). В этом случае свобода выбора раскрепощает детей, они деятельны и инициативны: даже слабоуспевающие учащиеся стараются не просто решить задачу, но решить ее несколькими способами.

Аналогично строится процесс овладения навыком решения задач на размещения. Стартовой служит задача про бутерброд: “Кот Матроскин стряпает двухслойные бутерброды, имея хлеб, колбасу и сыр. Сколько бутербродов сможет попробовать Матроскин? (Не забывайте, кот владеет секретом - ему не все равно, какой стороной бутерброд на язык класть!)”.

Моделирование процессов как методический прием очень эффективно при изучении данной темы. Оно позволяет учащимся с достаточной точностью глубины овладеть понятиями “комбинирование”, “выборки”, разобраться с различными видами выборок, осознать разницу между сочетаниями и размещениями, связь между размещениями и перестановками, научиться решать элементарные комбинаторные задачи.

Учащиеся выходят к доске, громко зачитывают классу записанную на карточке фразу и крепят карточку на шкалу так, как это кажется им целесообразно. Класс волен соглашаться или не соглашаться с оценкой достоверности рассматриваемого события, - ведется спор, страсти кипят. Вот к доске вышел Слава с карточкой про лужу, он крепит свою карточку в крайнюю правую позицию по шкале. Следуют активные возражения:

- Неправильно! Может, в этой луже и воды-то нет, одна грязь осталась. Значит, вымокнуть нельзя. Крепи карточку на “может быть”!

- А может и грязи уже нет, вся высохла - одна только корочка?! Давай - на “не исключено”. Слава пытается отстоять свой выбор оценки:

- У меня не написано, что лужа сухая!

- Что она сырая, у тебя тоже не написано!

Полемика завершается компромиссом, и карточка крепится посередине шкалы.

В процессе работы по оценке достоверности событий вспоминаем вместе с учащимися некоторые расхожие фразы: “маловероятно” (в позиции “сомнительно; вряд ли” на шкале), “50 на 50”, “равновероятно” (в позиции “невозможно; никогда”), “со стопроцентной вероятностью” (в позиции “конечно; обязательно”). Чтобы ускорить рабочий процесс, договариваемся кодировать некоторые оценки:

единицей, если достоверность оценивается “конечно; обязательно”;
нулем, если оценка “невозможно; никогда”;
дробью 1/2, если оценка расположена ровно посередине шкалы.

Какие обучающие задачи решает этот урок-аукцион?
Учащиеся мягко, в естественной форме общения, переходят от выборок к новому объекту исследований - событиям, вживаются в это понятие. Одновременно происходит процесс активизации интуитивной оценки вероятности наступления какого-либо события. Кроме того, работа с карточками, живая дискуссия по оценке достоверности событий, порождает у учащихся глубокую скрытую неудовлетворенность: процесс оценки неоднозначен; оказывается, одно и тоже событие может оцениваться по-разному, если оно рассматривается в различных обстоятельствах. Ситуация требует ясности, и эту ясность внесет следующий урок, на котором ребята познакомятся с понятием “опыт”.

Опыт наводит порядок в неопределенности условий, ведь условия опыта обговариваются заранее и остаются неизменными в процессе проведения испытаний. Так, опыт “я падаю в лужу, полную воды и грязи” позволит оценить событие “я стану мокрый и грязный” единицей, другой опыт - “я падаю на тонкую корочку сухой грязи, которая осталась от лужи” даст иную, но тоже однозначную оценку. Понятия “опыт” и “полная группа событий” вводятся без формальных определений на уроке-лаборатории. Учащиеся проводят опыт по бросанию монеты. В начале урока мы немного говорим об опыте вообще и закономерностях, которые он может выявить. Учащиеся приходят к выводу, что проявить себя закономерность может только при многократном повторении опыта.

Мы хотим провести опыт, заключающийся в одном бросании монеты, допустим 780 раз. В классе 26 человек. Стоит ли каждому учащемуся бросать свою монету 780 раз? Ребята, вполне оценив трудоемкость опыта, предлагают иную его реализацию: каждому достаточно бросить монету 30 раз, в итоге получится 30*26=780 исходов, которые и договоримся считать исходами опыта. Договариваемся проводить опыт единым образом: монета достоинством в 50 рублей бросается на парту, результаты опыта фиксируются в тетради.

Итак, опыт проведен. Значений исходов, как оказалось, два. Обсуждаем совместно вопрос: могут ли произойти другие события в нашем опыте, отличные от событий “выпала решка”, “выпал орел”? Учащиеся вспоминают о том, что монета может встать на ребро, например, если попадет в щель или будет долго катиться - до полной остановки - вдоль какой-нибудь преграды. Поскольку в условиях нашего опыта такого случиться не может, договариваемся событие “монета встала на ребро” не рассматривать в качестве исхода. Так вводится понятие полной группы событий (исходов).

Переходим к обработке результатов опыта - подсчитываем количество выпавших “орлов” и “решек”, допустим, выпало 380 “орлов” и 400 “решек”. И тут я озадачиваю ребят вопросом:

- Посмотрите на результат нашего опыта. Подумайте и дайте ответ: если мы проведем еще один такой опыт, что будет выпадать чаще - “орел” или “решка”?

До сих пор ответ был одним: едва я успеваю закончить формулировку вопроса, ребята дружно кричат:

- “Решек” будет больше!

- Почему?

- В первый раз было больше, значит и во второй будет больше!

- Чем же “решка” так выгодно отличается от “орла”, что выпадает чаще?

- Может любой из вас сказать мне: “Сейчас я брошу монету. Гарантирую выпадение “решки”?

- Не-е-ет.

- У чего же больше шансов выпасть в результате единственного бросания монеты - у “орла” или у “решки”?

- Они одинаковые - “орел” и “решка”. Нельзя заранее сказать, каким будет исход опыта.

Так мы приходим к понятию равной возможности исходов. Учащиеся сами пытаются дать определение равной возможности:

“Неизвестно, которое из этих событий старше”;

“Такие события происходят в опыте поровну, если не жульничать”;

“То одно чаще происходит, то другое, а какое когда точно - неизвестно”.

Интересно наблюдать процесс овладения учащимися вероятностными понятиями. Сегодня в “игре” “380 против 400” победила “решка”, но очень скоро ребята будут отвечать иначе: “исходы равновероятны”. Однако необходимо разрешить возникший конфликт, ведь действительно число триста восемьдесят меньше четырехсот. Использую такой прием. Говорю ребятам: “Представьте, что мы проводим с вами опыт, заключающийся в пяти подбрасываниях монеты. Результаты будем фиксировать шариками: возьмем два пустых стакана, и в правый будем откладывать шарик, если выпала “решка”, а в левый - если выпал “орел”. Положим, опыт проведен и мы имеем в правом стакане 3 шарика, а в левом - 2. Вы можете, глядя на стаканы определить, каких исходов случилось больше? Конечно. Бели же подбрасываний будет не 5, а 780, шарики придется заменить чем-то более мелким, например песчинками (иначе емкости стаканов просто не хватит). Опыт завершен, я знаю, что в одном стакане 380 песчинок, в другом - 400. Вы этого не знаете. Сможете вы на глаз определить, в каком из стаканов песчинок больше? Нет, количество песка будет вам казаться одинаковым. Значит, чем больше будет число испытаний, тем ближе будут значения выпавших “орлов” и “решек”. Пришла пора познакомить учащихся с понятием “вероятность”.

Английское слово Probability определило символ для обозначения вероятности. Рассматриваем опыт: одно бросание монеты. Рассмотрим событие А = “в результате опыта выпадет “орел” или “решка””. Это достоверное событие, оно произойдет обязательно, значит, пользуясь шкалой достоверности, можно сказать, что Р(А) = 1. Выпадение “орла” или “решки” - события равновозможные, других исходов опыта нет, поэтому Р( выпадет “орел”) = Р (выпадет “решка”) = 1/2.

О чем нам может поведать вероятность события равная 1/2? О том, что при большом количестве проводимых испытаний это событие произойдет в половине всех случаев.

Вопрос учащимся: “Бросается игральная кость. Какова вероятность выпадения 1 очка? Четырех очков?” Учащиеся, пользуясь методом аналогии, быстро находят ответ на первый вопрос и не попадаются “на удочку второго”.

Теперь учащимся предстоит “открыть” правило для вычисления вероятности наступления какого-либо события. Анализируем уже наработанную информацию.

Опыт - бросание монеты. Всего исходов 2. Интересующий нас исход “выпадает “орел” - один из двух возможных. Р= 1/2. Опыт - бросание кости. Всего исходов 6. Интересующий нас исход “выпадает четыре очка” - один из шести возможных. Р= 1/6. Что-то начинает светиться в глазах моих ребят, но в лицах - неуверенность. Необходима помощь. Я предлагаю решить еще одну задачу: “Опыт - бросание кости. Какова вероятность того, что выпадет четное число очков?” Рисуем дерево событий.

На кости могут выпасть следующие количества очков: 1,2,3,4,3,4,5,6. Четными в этой последовательности являются значения 2,4,6. Следовательно, искомая вероятность равна 1/6+1/6+1/6 = 3/6

Лица детей проясняются, разглаживаются, класс расцвечивается улыбками - поняли. Для закрепления решаем задачи, например, такую: "Найдите вероятность того, что при одном бросании число очков делится на три".

Чтобы обобщить полученные результаты, ввожу понятие "благоприятствующие исходы" и предлагаю обсудить формулу:

В дальнейшем при решении задач - чаще придуманных ребятами, реже предложенных мною (задачами обеспечиваем себя сами!) - ребята выбирают способ решения по своему усмотрению: графическое моделирование или использование формулы.

Урок "мера и вероятность", пожалуй, самый напряженный по интенсивности исследовательской деятельности учащихся. Увидеть связь между мерой и вероятностью, суметь выразить эту связь и проследить возможности ее использования - все это очень непросто. Используя интуицию, анализ, логику и обобщение, ребята проходят этот путь.

Схема овладения материалом выглядит так:

в формуле (1) обозначим буквой А множество всех исходов, благоприятствующих событию А, буквой W - множество всех возможных исходов данного опыта. Тогда формулу (1) можно будет записать в ином виде:

m (А)

Р(А)=     -----------------------

m (W )

Известный факт мы рассмотрим с новой позиции и получим новую формулу. Ставлю вопрос: “Что это нам дает?”

- Формула стала короче.

- Верно, еще что?

Предлагаю решить задачу про листок и колодец. “Колодец заткан паутиной. Лист, сорванный ветром с дерева, в этот колодец упал. Какова вероятность, что он долетит до воды?”

Случай а) не вызывает затруднений (срабатывает интуитивное понятие вероятности). Случай б) заставляет задуматься. Тишина может стать напряженной, но ее прервет-таки вопль: “Вижу!” или поднимется в сдерживаемом волнении чья-то рука. Начнет высказывать свои предположения один, туг же подключится другой, третий - узнали, увидели отношение мер бесконечного множества и его подмножества (тема “Множества”). Таким образом, новая формула через глубокое ее осмысление открывает шестиклассникам новые возможности - решение элементарных задач на геометрическую вероятность.

Овладение навыком решения простейших задач не является конечной целью изучения темы “Введение в теорию вероятностей”. Цель - в развитии вероятностного мышления учащихся, которое, в частности, позволит им выбрать собственную стратегию в игре (ребята должны уметь перебрать все возможные разрешения какой-либо ситуации, оценить их и выбрать оптимальный для данной игры вариант). Поэтому, в качестве логического завершения темы учащимся предлагается серия игр (одни из них предлагаются учителем, другие - самими учащимися). Рассмотрим два из них. Игра “Левый-Правый” - парная игра с использованием двух игральных костей. Игроки бросают кости, и если сумма выпавших очков 2,3,4,10,11,12, то один балл получает “Левый”, если сумма очков 5,6,7,8,9 -балл достается “Правому”.

Учащиеся делают необходимые вычисления и делают вывод: в этой игре лучше выбрать роль “Правого”. Вывод должен быть подтвержден в ходе контрольной игры.

Аналогично проводится игра “Король и Звездочет”. Суть этой игры в следующем: Король решает судьбу провинившегося звездочета. Приготовлено две вазы, и четыре шара (2 белых и 2 черных) помещаются в эти вазы. Король наудачу вынимает шар из выбранной наугад вазы и решает судьбу звездочета: белый шар сохранит Звездочету жизнь. Вопрос для учащихся: “Мы можем помочь Звездочету. Как стоит разложить шары по вазам, чтобы шансы Звездочета уцелеть были наибольшими?”

Ребята моделируют раскладки шаров, подсчитывают в каждом случае вероятность того, что наудачу извлеченный шар окажется белым, оценивают найденные вероятности и принимают решение: оптимальным является разложение (ч,ч,б) и (б). Подтверждением служит контрольная игра (или несколько игр).

Количество шаров и ваз можно менять, усложняя таким образом условия игры.

Вопрос о частоте наступления какого-либо события рассматривается на практическом материале, который накапливается учащимися в результате проведения серии контрольных игр. Так, в стартовой игре “Король и Звездочет” (2 вазы и 4 шара) вероятность события “Звездочет уцелеет” при раскладе (ч,ч,б) и (б) по вазам равна 2/3. В одной из контрольных игр при этом раскладе “уцелело” 18 “Звездочетов” из 26. Таким образом, уже можно говорить о частоте наступления события “Звездочет уцелеет” в данном опыте.

В ходе изучения данной темы особенно хорошо заметны развитие мыслительных способностей учащихся и возрастание их интереса к исследовательской деятельности.

Тема пятая: “Случайные числа”.

Тема начинается с очень интересного вопроса - магии чисел. Учащиеся вместе с учителем совершают экскурс в историю развития чисел, узнают, что такие привычные, давно и хорошо известные им числа: 1, 2, 3, ..., 7 обладают волшебной силой. Этот факт подтверждается обширным фольклорным материалом: ребята подготавливают и проводят аукцион пословиц, поговорок, загадок, в которых упоминаются магические числа.

Путешествие в волшебную страну чисел продолжается знакомством с упорядоченными наборами чисел - последовательностями. Учащиеся выполняют задания на поиск закономерностей в предложенных 32 последовательностях, сами составляют последовательности. После этого ребята знакомятся с упорядоченными таблицами (таблицами неслучайных чисел). Затем перед учащимися ставится следующая задача: необходимо составить таблицу, не являющуюся закономерной (таблицу случайных чисел). Работу по созданию такой таблицы проводим сообща: учащиеся называют числа, учитель записывает их в таблицу на доске. Скоро выясняется, что зависимость все-таки имеет место, и хотя таблица не является закономерной, случайной ее тоже назвать нельзя. Чем больше чисел уже записано в таблице, тем неслучайность ее очевидней: ребята медлят с “выдачей” числа, они тратят время на просмотр уже записанных элементов, им непременно хочется “выдать” что-нибудь необыкновенное, отличное от имеющегося. Таким образом, шестиклассники убеждаются, что с поставленной задачей им не справиться. Так они подводятся к идее создания прибора - генератора случайных чисел (ГСЧ). Простейшими ГСЧ могут служить монетка, кубик, и учащиеся с их помощью заполняют таблицу случайными числами.

Домашняя работа заключается в конструировании и изготовлении генераторов случайных чисел. Генераторы будут необходимы учащимся для лабораторной работы - с помощью своих ГСЧ ребята конструируют свои таблицы случайных чисел. В процессе эксплуатации учащиеся находят недочеты в конструкциях своих ГСЧ и, как правило, к следующему занятию либо усовершенствуют свои генераторы, либо конструируют и изготавливают новые, более сложные. Это радует - тяга к творчеству, умение ставить перед собой цель и достичь ее, очевидно, преобладают в этом случае над другими качествами ребенка, ведь, по сути дела, ребята сами (не учитель) задают себе домашнее задание, сами выполняют его со всем старанием, чтобы начатое дело было доведено до конца наилучшим образом.

ГСЧ годится не только для таблиц. Оказывается, он готов снять с человека ответственность за выбор решения. Учащимися предлагаются игры с использованием ГСЧ. Например, в игре “Лабиринт” ГСЧ определяет направление движения по переходам лабиринта. Лабиринт полон ловушками и тупиками, но ГСЧ бесстрастно отправляет на “верную гибель” тех, кто вверил ему свою судьбу.

ГСЧ используется не только в игре. С его помощью можно моделировать некоторые случайные процессы. Учащимся предлагается промоделировать движение на доске Гальтона десяти брошенных шариков (если ГСЧ выдает четное число - шар движется вправо, в противном случае - влево).

В целом курс “Закономерности окружающего мира - 6” и методика преподавания курса имеют целью не только развитие вариативного мышления учащихся, их способностей к адаптации в условиях непрерывного изменения окружающей реальности, но и воспитание в ребенке уверенности в своих способностях, самоуважения, формировании здоровой “я - концепции”, осознанию необходимости открытых связей между людьми.