Уровень овладения моделированием должен занимать особое и главное место в формировании умения решать задачи. Обучение моделированию необходимо вести целенаправленно, соблюдая ряд условий.
Во-первых, все математические понятия, используемые при решении задач должны изучаться с помощью моделей. Во-вторых, должна вестись работа по усвоению знаково-символического языка, на котором строится модель. При этом ученик осознает значение каждого элемента модели, осуществляя переход от реальности (предметной ситуации) к модели, и наоборот, от модели к реальности. В-третьих, необходимый этап обучения - освоение моделей тех отношений, которые рассматриваются в задачах. Только освоив модель отношений (т.е. осознав суть этого отношения), учащийся научится использовать её как средство выделения сущности любой задачи, содержащей это отношение.
Чтобы самостоятельно решать задачи, ученик должен освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче, и переходить от одной модели к другой.
Необходимо отметить, что в данной работе я не касаюсь краткой записи условия задачи. Этот этап очень важен, однако, я исходила из того, что он традиционно присутствует в работе учителя. Поэтому главное внимание я уделяю тем приемам работы над задачей, которые в меньшей степени используются в традиционной системе, которые помогают мне пробудить у детей интерес к задаче, к поиску решений этой задачи.
При решении простых и составных задач на сложение и вычитание используется схематический чертеж.
Схематический чертеж прост для восприятия, так как:
- наглядно отражает каждый элемент отношения, что позволяет ему оставаться и при любых преобразованиях данного отношения;
- обеспечивает целостность восприятия задачи;
- позволяет увидеть сущность объекта в "чистом" виде без отвлечения на частные конкретные характеристики (числовые значения величин, яркие изображения и др.), что трудно сделать, используя другие графические модели;
- обладая свойствами предметной наглядности, конкретизирует абстрактные отношения, что нельзя увидеть, например, выполнив краткую запись задачи;
- обеспечивает поиск плана решения, что позволяет постоянно соотносить физическое (или графическое) и математическое действия.
Как было сказано выше, текстовые задачи на сложение-вычитание в 1-м классе строятся как частные случаи отношения величин, поэтому моделирование простой задачи у детей не вызывало затруднения, т.к. величины в задаче находятся в отношении целого и частей (см. Рис. 3.).
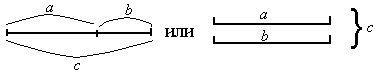
Если величины связаны отношением "больше (меньше) на" (Рис. 4.); Сравнение двух величин (Рис. 5.).
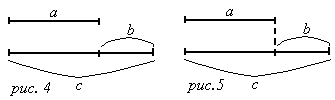
Со схемами в системе Д.Б.Эльконина-В.В.Давыдова дети знакомятся с первых уроков, когда находят среди разных предметов одинаковые по какому-либо признаку: длине, площади, форме, объему.
Учащимся выдается набор полосок разных по длине, ширине и цвету. Их задача найти равные по какому-либо признаку. Сразу дети находят одинаковые по цвету, затем, путем наложения, одинаковые по длине. Перед учащимися ставится следующая задача:
- Что нужно сделать, чтобы каждый раз не измерять полоски, а найти одинаковые сразу и быстро? Дети предлагают свои варианты: различные значки, но значки должны быть одинаковые, и на одинаковых полосках ставят значки.
- А как записать в тетради, что среди полосок есть одинаковые?
Ребята обсуждают задание и приходят к выводу, что нужно зарисовать и поставить значки.
Далее дети выполняют более сложное задание: сравнивают сосуды по объему и находят равные. Равные сосуды необходимо запомнить, а лучше как-то отметить. Опять предлагаются значки.
Затем записывают в тетради с помощью рисунка и значка, что на столе есть одинаковые по объему сосуды.
После этого дети находят сосуды, одинаковые по другим признакам: материалу и высоте. Записывают в тетради, что сосуды равны по высоте с помощью вертикальных отрезков.
На последующих уроках дети с помощью схем учатся находить и определять равные и неравные величины (С задания 13. Номера взяты из учебника "Математика 1 класс" Захаровой A.M., Фещенко Т.И.), показывать с помощью схем равенство и неравенство величин (Рис. 6).

Через несколько уроков вводится буквенная символика. Все величины обозначаются буквами русского алфавита.
На уроке с помощью весов ученики устанавливают, что масса банки с водой и мешочка с песком одинакова. Затем дети записывают равенство масс с помощью отрезков равной величины. Обсуждая схему, дети приходят к выводу: величины необходимо обозначить, чтобы было понятно и другим людям. Учитель предлагает обозначить с помощью букв. Буквы подписываются и на предметах и на схеме (Рис.7).

Делается вывод, что о равенстве величин можно сказать формулой: А = Б. (Масса "А" равна массе "Б").
Итак, выполняя предметные действия (на основе измерения разных величин), отображая эти действия графически, сначала в виде рисунка, затем модели, учащиеся подходят к знаково-символической форме: равенству, уравнению.
В задании 60 дети знакомятся с понятиями "целое" и "части". Свои практические действия они переносят на бумагу с помощью схем.
В этой теме появляются текстовые задачи и уравнения, которые решаются с помощью, с опорой на схему. Работа со схемой в текстовых задачах является продолжением, а не новым материалом, как в традиционной системе, поэтому проходит легче, вызывая у детей интерес. Очень важно этот интерес у детей поддержать различными видами работ со схемой, которые помогли бы ребятам выбрать правильное решение задачи. Поэтому, на мой взгляд, необходимо, чтобы схему дети составляли сами, без помощи учителя.
1. Составление схемы
К кормушке прилетело И синиц и К воробьев. Сколько всего птиц в кормушке?
На доске вычерчиваются все схемы, которые предлагают ребята. Каждая схема анализируется. После анализа остаются правильные, из которых выделяется более удобная для выбора решения (Рис.8).
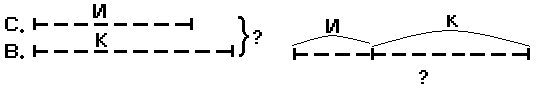
Из группы схем дети выбирают нужную (Рис.9).
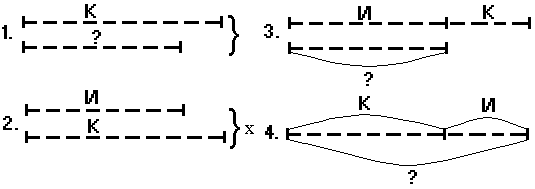
Выбрав схему 4, учащиеся объясняют решение задачи: все птицы - это целое, которое состоит из двух частей: воробьев и синиц, поэтому, чтобы найти, сколько всего птиц, нужно сложить К+И.
2. Анализируя после решения задачи схему 2, можно перейти к составлению уравнений:
х - И = К х = К + И
х - К = И х = И + К.
3. Активно проходит работа по составлению задач по схеме (Рис.10)
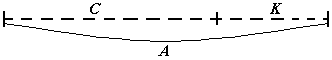 |
С + К = А, А - С = К А - К = С. |
4. С помощью схемы можно дать понятие обратной задачи. Дети решили задачу:" В кормушке было А воробьев, прилетели синицы и стало М птиц. Сколько птиц прилетело?" (см. Рис. 11).
 |
A + x = M x = M - A. |
Затем схема меняется (Рис. 12).
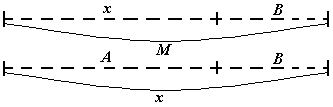 |
x + B = M x = M - B x = A + B |
По схеме дети должны изменить условие задачи и уравнение к ней.
Во 2 - 4 классах работа над схемой продолжается. При решении составных задач схема помогает не только найти различные способы решения, но и выбрать самый рациональный, самый короткий. Например:"На трех полках стояло 116 книг. Когда с первой полки сняли 8 книг, со второй - 12 книг, а с третьей - 6 книг, на всех полках осталось поровну. Сколько книг стояло на первой полке первоначально?"
Строится схема (Рис. 13).
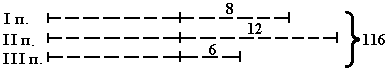
Дети анализируют задачу, а затем предлагают свой способ решения. Обычно средние и слабые ученики предлагают:
8 + 6 = 14 или 116 - 8 = 108
14 + 12 = 26 108 - 12 = 96
116 - 26 = 90 96 - 6 = 90
90 : 3 = 30 90 : 3 = 30
30 + 8 = 38 30 + 8 = 38
Сильные ученики предлагают свой вариант решения:
12 + 8 + 6 = 26
116 - 26 = 90
90 : 3 = 30
30 + 8 = 38
Все способы анализируются и выясняется, что все решили правильно. Выбирается самый рациональный. Те ребята, которые решили задачу рациональным способом, объясняют, что им помогло выбрать этот способ. (По схеме видно, что все книги состоят из 2-х частей, тех, что сняли и тех, которые остались на полках. Все книги, которые сняли - это целое. Целое состоит из 3-х частей, снимали с трех полок, а целое мы узнаем действием сложения, складываем все части).
При решении задач на умножение и деление первоначально использовали чертеж.
"В одной коробке 6 карандашей. Сколько карандашей в 3 таких коробках?" (Рис. 14)

Использовался чертеж и при решении задач на пропорциональное деление. Например: "Одно число больше другого в 6 раз, а их сумма составляет 350. Найти числа." (Рис.15).
При решении задач на движение в схему были сразу введены условные обозначения: S - сплошная дуга, V - стрелка, t - пунктирная дуга.
"Навстречу друг другу одновременно из двух деревень вышли две пешехода. Скорость одного из них 5 км/ч., а другого 4 км/ч. Через 2 час они встретились. Какое расстояние между деревнями?" (Рис. 16).
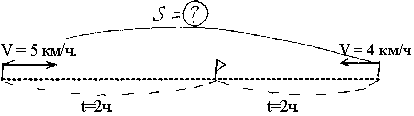
Четкие условные обозначение позволяют детям строить сложные схемы, видеть в них нужные формулы, отношения для решения задачи. Иногда мелочь в условных обозначениях, в схеме, позволяет не запутаться в числовых значениях составной задачи. Так при решении задач на приведение к единице обозначение количества пунктирной дугой (на начальном этапе решения таких задач) позволило более четко представлять условие задачи и не путаться в числовых данных.
Например: "Для детского сада купили 25 мячей по 4000 рублей и 10 мячей по 7000 рублей. Сколько денег заплатили за все эти мячи?" (Рис.17).
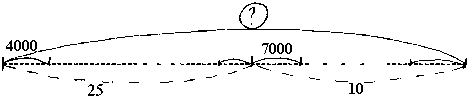
Из всего выше сказанного видно, что схема в развивающем обучении имеет очень большое значение и для решения задач и для составления и решения уравнений, и для решения текстовых задач способом составления уравнений.
Первое уравнение составляется только по схеме и решается с опорой на схему (Рис. 18).
 |
X + A = B X = B - A. |
Ученики по чертежу устанавливают, что х - это часть. Чтобы найти часть, нужно из целого вычесть известную часть А.
И в 3 - 4 классе, когда изучаются свойства уравнения, схема снова приходит на помощь в проверке уравнений при доказательстве свойств.
| Решается уравнение: |
5 + x - a = c x = c + a - 5. |
Затем с помощью схемы проверяется: (Рис. 19).
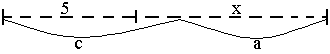 |
x = c + a - 5 |
Схемы помогают и при решении задач способом составления уравнения. С помощью схемы составляются уравнения к задачам.
Например: "За лето собрали 36 кг. 800 гр. лекарственных растений. Их них 12 кг. 250 гр. Липового цвета, листьев крапивы на 3 кг. 130 гр. Меньше, чем липового цвета, а остальное ромашка. Сколько килограммов ромашки было собрано?" Составляется схема.

I + II + III = 36800
х - III
12250 - 1
12250 - 3130 - II
12250 + 12250 - 3130 + х = 36800
При составлении уравнений к задачам, как и при решении задач на "приведение к единице", помогает краткая запись в виде таблицы. По таблице ребята находят равные величины или величины , которые можно уравнять.
Например: "За несколько пар коньков ценой 5000 руб. Заплатили 20.000рублей, а за столько же пар ботинок 96.000руб. Сколько стоила пара ботинок?"
| Цена | Количество | Стоимость | |
| II | 5000 | I = II | 20.000 |
| I | ?(х) | I = II | 96.000 |
Одинаковая величина - количество. Эту величину уравнивают, составляя уравнение:
I = 20.000 : 5.000 II = 96.000 : х
20.000 : 5000 = 96.000 : х
Способ краткой записи: таблицы или схему дети выбирают сами, если предлагают обе, то обе выносятся на доску, обсуждается, что больше помогает найти решение задачи или составить уравнение. Такая работа проводится на начальном этапе, а затем при решении задач ребенок сам для себя выбирает удобный способ записи условия задачи.