ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 2 Дидактический материал

Примеры 1-10  

Пример 1
Какие процессы изменения во времени вы назовете непрерывными, какие дискретными?
а) изменение годового остатка на вкладе в банке;
б) угла поворота вала со временем;
в) объема воды в заполняемом резервуаре;
г) численности населения, регистрируемой по ежегодной переписи;
д) координаты движущейся материальной точки;
е) мгновенной скорости материальной точки;
ж) годового валового продукта экономики в стоимостном выражении;
з) тока в электрической цепи;
и) массы ускоряемой элементарной частицы;
к) энергии молекулы в идеальном газе при соударении с другими молекулами;
л) координаты движущейся материальной точки при стробоскопическом освещении;
м) потенциальной энергии санок, съезжающих с горки с фигурным профилем
н)* энергии частицы в плазме (ионизованное состояние газа).

Пример 2.
Запишите формулы для следующих процессов изменения:
а) координаты при равномерном движении;
б) величины долга при простых процентах;
в) угла поворота вала при равномерном вращении;
г) величины вклада при сложных процентах;
д) смещения материальной точки при гармонических колебаниях;
е) координаты при равноускоренном движении;
ж) координат при равномерном вращении точки на плоскости;
з)* координат при равномерном движении вверх по правой спирали;
и)* числа ежегодно продаваемой фирмой автомобилей, если оно увеличивается всякий не високосный год на 2%, а в високосный— не увеличивается.
Указание. Все необходимые величины и параметры вводят и мнемонически обозначают сами школьники.

Пример 3.
Найти формулу общего члена последовательностей:
а) 1,-2,3,-4; б) ; в); г) 1,-1,2,-2,3,-3;

д) 1,3,9; е) 1;0;2;0;3;0...; ж) 0,1,1,2,3,5,8...; з) ;

и) .
к) .
Всегда ли можно найти такую формулу в компактной записи? Всегда ли эта формула находится однозначно по первым нескольким членам?

Пример 4. (метод неопределенных коэффициентов)
На примере последовательности д) из предыдущего номера продемонстрируйте, что существует бесконечно много последовательностей полиномиального типа , первые члены которой суть 1,3, 9. Что можно сказать об остальных последовательностях? Однозначно ли их продолжение?

Пример 5.
Исследуйте на монотонность и на существование предела последовательности из № 3.

Пример 6.
Докажите, что последовательность, заданная формулой монотонно и неограниченно возрастает.
Указание. Рассмотреть и сравнить с единицей отношение a_n+1/a_n.

Пример 7.
Сравните монотонные последовательности по скорости убывания и роста.
а) ; б)  ; в) ; г) ;
д) ; е) ; ж) ; з) ; и) .

Пример 8.
Найдите предел последовательности
Ответ. 1/k!.
Методические замечания. В предыдущих примерах представлены последовательности, описывающие практические все виды поведения процессов: рост, убывание, осцилляция, выход на насыщение, катастрофическое поведение и др. При решении по возможности надо сообщать учащимся, какая величина (из физики, экономики и т. д.) ведет себя по аналогичному закону.

Пример 9.
Алгебраист дал Логику задание: решить уравнение .
Однако, Логик, как узкий специалист, забыл формулу корней, но рассудил следующим образом. Из уравнения следует: тогда . Найдем, решил, хотя бы положительный корень, тем более, из графического построения видно, что он не более двух. Тогда, по логике (по Логику) , далее и т. д. Чем дальше расположен , под последним радикалом, тем меньше от него зависит значение всего выражения. Тогда достаточно взять x равным единице при достаточном числе радикалов — и хорошая точность будет обеспечена. Прав ли Логик? Ответ обоснуйте, используя понятие производной, как скорости изменения функции. Проверьте сколько радикалов необходимо взять в «формуле Логика», чтобы обеспечить точность в 3-м знаке после запятой.
Замечание. Этот “несерьезный” пример иллюстрирует идею метода последовательного приближения (метод итераций) при решении многих математических задач, и не только для нахождения корня уравнения. По сути, такой прием используется в т. н. теории возмущений.

Пример 10.
1) Найдите бесконечное произведение .
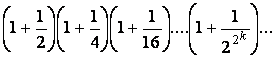2) Объясните, как вы понимаете этот термин, и составьте соответствующую рекуррентную последовательность (2 способа).
Ответ: 1) 2.

(Пример 1-10, 11-20, 21-30, 31-40, 41-55)

Содержание

вернуться на страницу Дистанционная поддержка