ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 2 Дидактический материал

Примеры 31-40  

Пример 31
Запишите в матричной форме рекуррентные соотношения для фибоначчиевых и «антифибоначчиевых» чисел и найдите решения при известных начальных условиях.
Решение. Рекуррентные соотношения имеют вид . Рассматриваем пару последовательных чисел как координаты геометрического вектора на плоскости 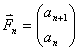. Тогда нетрудно получить 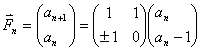, или , «+» — для чисел Фибоначчи, «-» — анти-Фибоначчи.
Тогда любая пара чисел выразится через начальные значения мультипликаторным соотношением, напоминающим формулу общего члена геометрической прогрессии,

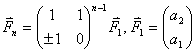
Методические замечания. 1) Предмет, разумеется, не может включать в себя материал по приведению матрицы к диагональному/жорданову виду и легкому вычислению тем самым любой ее степени. Об обратной матрице дается иллюстративно только понятие. При вычислении членов с большим номером важно научить, как это сделать оптимальным способом, развивая тем самым общее умение решать проблемы. Так, например, если номер n = 1025 — число, близкое к степени двойки, то 1024-ю степень матрицы легко получить 4-х кратным последовательным возведением ее в квадрат с фиксацией промежуточного результата, а затем умножением на 4-ю степень.
2) На этом примере учащиеся убеждаются, что любое линейное однородное рекуррентное соотношение разрешается через возведение матрицы в степень и последующим умножением на вектор начальных условий. Тем самым повышается важность понятия геометрической прогрессии, как результата действия одномерного матричного мультипликатора.
3) При высоких степенях характеристического уравнения его решить невозможно (теорема Абеля), только приближенно, да и корни могут оказаться комплексными. Матричный способ дает альтернативный путь, переводящий задачу в плоскость абсолютно точно реализуемых, пусть объемных вычислений, и проблема возникает в их эвристической оптимизации.
4) На данном примере школьники учатся правильно выбирать набор и структуру моделируемых величин (причем не одномоментных, но разделенных во времени!) и устанавливать соотношения между ними. Инструментами здесь являются хорошо знакомый вектор и вновь введенная матрица.
5) Интересно проследить траектории этих двух последовательностей на плоскости при помощи компьютерной графики. Точки первой при больших значениях номера n, отдаляясь от начала координат, будут приближаться к прямой y=λx+B, λ=λ₁ или λ₂ — корни векового уравнения, у второй — поворачиваться вокруг начала координат.

Пример 32. (Геометрия комплексных чисел)
При помощи циркуля и линейки на комплексной плоскости для данного z (например, 1+2i) постройте а) z*; б) (z+z*)/2; в) (z-z*)/2 г) 1/z; д)√z.
Решение. Рассмотрим п.г). Построение возможно двумя способами.
Первый способ опирается на следствие из теоремы Фалеса и том факте, что 1:z =1/z:1.
Другой способ заключается в следующем. Проводится вектор из начала координат в точку z — Oz. Проводится циркулем единичная окружность С₁ c центром в начале координат. Восстанавливаются перпендикуляры h к Oz в т.O до пересечения с С₁. Через т. z и тт. пересечения h и С₁ проводится окружность С_z. Пересечение ее с продолжением вектора Oz дает -1/z*. Инверсией относительно начала координат и симметрией относительно действительной оси получаем 1/z. (Обоснуйте самостоятельно этот метод.)
Пункт д). Вектор Oz продолжается за начало координат на единичный отрезок, т. е. до пересечения с С₁ в т. B. К середине отрезка Bz восстанавливается перпендикуляр длиной Bz/2, и проводится окружность С₃ через концы отрезка Bz и конец перпендикуляра. Восстанавливается в начале координат другой перпендикуляр к Bz до пересечения с С₃ в т. D. Проводится биссектриса угла zOx и продолжается за начало координат. По обе стороны на ней откладываются отрезки OD. Это и есть два корня из z.

Пример 33.
Составьте матричную модель инвестиционной экономики (см. пример № 22) и запишите ее решение в матричном виде.
Решение.

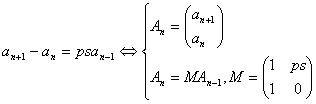
Тогда 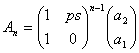. Матрица M — мультипликатор экономики.
Другой путь — введение вектора, координаты которого суть валовой продукт и инвестиции,—

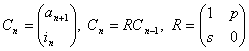
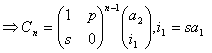
Пример 34. (комплексные корни)
Найдите формулу общего члена для анти-Фибоначчиевых чисел, но с начальными условиями a₁ = 1, a₂ = i и переведите ее в матричное представление.

Пример 35.
Велосипедист, стоя на беговой дорожке, заметил, что в 36 метрах от него к нему приближается бегун с постоянной скоростью v, и начал отдаляться от него с постоянным ускорением a =0.5 м/c². Бегун догнал велосипедиста, но не смог его обогнать. Чему равна скорость v?
Указание. Задача демонстрирует механическую интерпретацию касательной к параболе.

Пример 36.
Материальная точка движется по графику функции в сторону возрастания абсциссы x. 1) Найдите координаты вектора ее мгновенной скорости в тот момент, когда она пересекает ось Ox, если известно, что ее величина равна м/с. 2) Найдите координаты вектора ускорения a м/c² точки, если известно, что он образует с вектором скорости угол a= arctg(7/6) (против часовой стрелки), и по модулю равен м/с^2.
Методические замечания. Задача одновременно на криволинейное движение, на решение уравнений высоких степеней, на геометрический и механический смысл производных и их приложение к геометрическим векторам.
Решение. 1) Простой, т. е. некратный корень x =1 легко угадывается по сумме коэффициентов. При делении левой части на x-1 получается полином P₄(x)= x⁴+3x³+3x²+3x+3= x⁴+3( x²+1) (x+1). Второе слагаемое положительно при x>-1, а первое — неотрицательно. Следовательно, еще корни могут быть только при x<-1.
Производная обращается в нуль в двух точках d₁=0 и d₂=-8/5. Предположим есть еще отрицательный корень x₂. Тогда .
Рациональное d₂=-8/5 не может быть корнем уравнения, т. к. 8 — не делитель 3-х. Следовательно, кратных корней исходное уравнение не имеет. Тогда из-за множителя –многочлена нечетной степени P₃(x) должен быть еще и третий корень, тоже меньший и –1, и –8/5. Но —

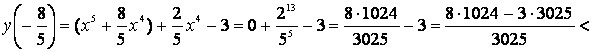
А на луче (-∞;-8/5] функция y(x) возрастает, следовательно, она отрицательна, и корней нет.
Наше предположение о наличии еще хотя бы одного корня привело к противоречию с фактами, следовательно, оно неверно, и корень x=1— единственный.
Производная является тангенс угла наклона вектора скорости к Ox.

Тогда координаты суть 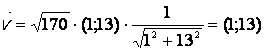м/с.
2) По формуле тангенса суммы легко находится угол наклона вектора ускорения с осью абсцисс.
Он равен p/4, а координаты a =(2;2) м/c².

Пример 37.
При каких значениях уравнение имеет ровно два корня?
Решение. Решаем методом семейств однопараметрических линий. Изолируем параметр в правой части вместе с неизменным свободным членом:
График левой части уравнения — «парабола» 5-й степени; левой части соответствует семейство прямых (фокус), проходящих через т. A(0;-1) (Рис.1).

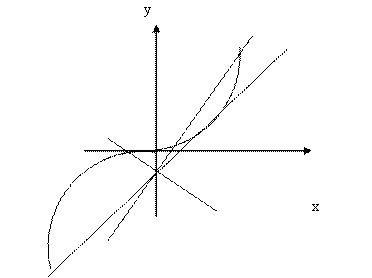
Рис.1.

Уравнение имеет ровно два корня, когда прямая y₁ = – 1+ax касается графика y₂ =x⁵. В точке касания равны значения функций и их производных

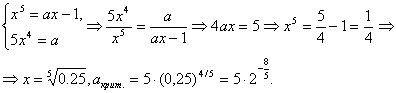
При изменении a от −∞ до +∞ прямая поворачивается вокруг т. A(0;-1), до достижения критического значения параметра уравнение имеет один корень, при критическом значении — два, при значении, превосходящем критическое — три.

Пример 38.
Для каждого из семейств линий составьте универсальное соотношение между задающей функцией и ее производной:
а) y = x+C; б) y = (x+C)²; в) y =Cx; г) y =C/x;
д) ; е) ; ж) ; з) ; и) ; к) .
Изобразите эти семейства на плоскости.
Решение. Производная функции и сама функция, определяющая семейство, связаны между собой через параметр C. Его необходимо исключить. Делается это следующим образом (пункт г):

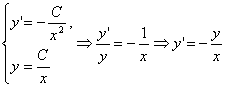
Замечание 1. Это известный прием «зачистки» лишней неизвестной, такой же, как и при решении текстовых задач на составление моделей, когда введено переменных больше, чем надо. Но применен он не «забавы ради» (из пункта A путешествующие велосипедисты, трубы, наполняющие бассейн и пр. благоглупости), но ради открытия (читай Д. Пойа!) школьниками математической истины.
Ответ:з) ; и) ; к)
Замечание 2. Обратить внимание на то, что кроме случаев б) и з) связь между y’ и y выражается линейным соотношением, но с «коэффициентом», зависящем от x.

Пример 39. (Мини-проект на дом)
1) Убедитесь, что касательная, проведенная из начала координат к любой из линий семейства , касается последней в точке с ординатой, равной числу Эйлера e. 2) Составьте дифференциальное соотношение для этого семейства. 3) Экспериментально графически найдите число e и сравните с табличным значением.
Решение. П.1) В точке касания M(x0,y0) равны значения функции и касательной y = kx, а также их производные:

П.2) Прологарифмируем задающее функцию выражение и получим
.
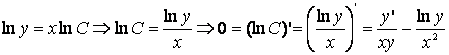
После несложного преобразования — .
П.3) Учитель индивидуально дает учащимся значение основания С. Предпочтительные значения — 2, 9/4, Ö2, Ö3, 3 и им обратные: ½, 4/9 и т.д.

Пример 40. (Движение с сопротивлением)
Водитель катера, двигающегося в неподвижной воде, заглушил мотор на скорости v₀= 36 км/ч. Сила сопротивления воды определяется как F_сопр.=-kvⁿ, k = 1000 Н/мⁿ, масса катера с водителем m = 1 т. Найдите законы изменения скорости и тормозные пути катера для n = 1 и 2. Постройте графики и проанализируйте полученные результаты.
Указание. Для нахождения общих решений использовать знания об однопараметрических семействах линий.
Решение. Уравнение движения лодки.
Для n =1 . Мы знаем по семействам линий, что такому соотношению удовлетворяют функции вида . Из начальных условий получим C= v₀= 10 м/c,
пройденный за время t путь — .
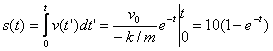Теоретически катер никогда не остановится (v(t)≠0), т. е. тормозное время бесконечно, но тормозной путь не превысит 10 м., т. к. второе слагаемое в скобке стремится, притом быстро, к нулю. Но реально уже через 10 секунд скорость будет измеряться долями миллиметра в секунду, т. е. практически нуль. Тормозной путь при этом составит 10 м. Нетрудно видеть, что он пропорционален произведению массы на начальную скорость, т. е. начальному импульсу, и обратно пропорционален коэффициенту сопротивления k.
Качественно иная ситуация для другого закона с n =2: .
Мы знаем, что такому условию удовлетворяют функции семейства 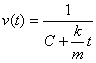. Из начальных условий получим C= 1/v₀= 0.1 с/м, и закон движения .
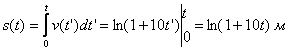Такой вид закона предполагает не только бесконечное тормозное время, но и бесконечный тормозной путь, т. к. логарифм неограниченно возрастает при t→∞. Реально, скорость упадет до порядка мм/с за 1000 секунд (16 мин), и путь составит чуть более 9 м.
В природе сила сопротивления движению со стороны жидкости (воды, газа) пропорциональна скорости v для малых значений последней, для бòльших значений v показатель степени n увеличивается до 2 ÷ 3 (Почему?). При скоростях, близких к звуковым, она возрастает еще более стремительно. Но именно линейный начальный участок на графике F_сопр(v) обеспечивает конечность тормозного пути.
Подобного рода соображения говорят в пользу многих линейных законов (Ома, Гука и др.), экспериментальная проверка которых сопряжена с проблемой точности, идеальности условий эксперимента, неоднозначностью интерпретации результатов и т. д. Следующий пример демонстрирует, что будет, если сила сопротивления изменяется по степенному закону с ростом скорости, но при показателе меньше единицы.
 

(Пример 1-10, 11-20, 21-30, 31-40, 41-55)

Содержание

вернуться на страницу Дистанционная поддержка