ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 2 Дидактический материал

Примеры 11-20  

Пример 11
При помощи бухгалтерского калькулятора найдите с точностью до 4-го знака после запятой положительный корень уравнения .
Указание. Корень четвертой степени на таком калькуляторе есть двукратное применение операции корня квадратного.
Методические указания. Это задание на составление алгоритма решения проблемы при известной общей идее. Но от идеи до надежного воплощения не близко. Ученик должен продумать ход выполнения этой лабораторной мини-работы с документированием промежуточных результатов в виде таблицы и проверкой их на валидность, т. е. на выполнение условий по точности. Должно быть продумано каждое нажатие на клавишу и возможность сохранения промежуточного результата на случай ошибочного действия.

Пример 12. (Вперед в прошлое)
Последовательность a_n, n=1,2,3….удовлетворяет условию Фибоначчи. Найти ее первый член, если a₁₀ = 2, a₈=3.
Решение. Легко найдем, что a₉=-1. Последовательность можно восстановить до первого члена банальным пересчетом:
a₇= a₉- a₈=-4, a₆= a₈ - a₇= 7, a₅= a₇ - a₆= -11, a₄= a₆ - a₅= 18, a₃= a₅ - a₄= -29, a₂= a₄ - a₃= 47, a₁= a₃ - a₂= -76.
Однако, в случае номеров, много больших чем 10, этот прием — пустая трата времени на арифметику. Рассмотрим первые 10 членов в обратном порядке как новую последовательность bn₌ a_10-n+1, n =1,2,3…10. Для нее справедливо рекуррентное соотношение .
Стандартный поиск решения в виде дает вековое уравнение с корнями .
Тогда общий вид решения 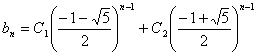. Из начальных условий b₁=a₁₀ = 2, b₃= a₈=3 (b₂= a₉ =-1) получим

.

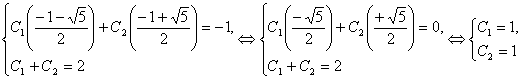
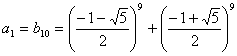По форме, мы нашли ответ и показали, что эта «грозная сумма» степеней равна -76.
Если же, ответ в приемлимом виде нам не известен, то мы можем подсчитать эту сумму, но не в лоб, а используя теорему Виета и свойства т. н. симметрических многочленов:


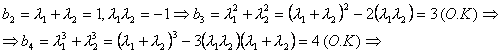
Методические замечания.
1) Подобного рода задачи, которые можно решить разными способами, включая элементарный подсчет, если не формируют чувство успешности у учащегося, то хотя бы не дают обратный эффект.
2) Здесь к счастью вычисления ограничились двукратным возведением в куб суммы корней. Перед учащимися можно поставить проблему кратчайшего вычисления суммы более высоких степеней, например, 108-ых.
Проблема имеет творческий характер и развивает числовые комбинаторные способности. Школьник должен сообразить, суммами каких степеней он должен оперировать, чтобы поскорее добраться до 108-ой. Например, если третьими, то мы дойдем до 81-й за 3 шага. Необходимо еще повысить степень на 27 единиц (как получить?). Комбинационно возникает 54-я степень, которую можно получить, возводя в квадрат сумму 27-х степеней.

Пример 13. (Прогрессия или не прогрессия?)
Как известно, любой средний член арифметической прогрессии (АП) есть полусумма равноотстоящих от него членов Следовательно, Наоборот, любая ли последовательность, удовлетворяющая последнему уравнению, является АП?
Методические указания и решение. Решение приводит к т. н. возвратному характеристическому (вековому) уравнению, два кратных корня которого λ₁=λ₂=1 легко угадываются, исходя из того факта, что среди всех возможных решений (т.н. общего решения) соответствующего уравнения обязательно есть арифметические прогрессии. (Кратность корня также можно продемонстрировать путем взятия производной от левой части уравнения, которая также должна обращаться в нуль.)
Два оставшихся — λ₃ = 1/λ₄ = (-3+√5)/2 определяют знакочередующиеся геометрические прогрессии: убывающую и возрастающую. Таким образом, при должным образом подобранных начальных условиях (НУ) мы всегда будем иметь дело с прогрессиями, при произвольных НУ — с их суммами.
Решая, разбирая эту задачу, учащиеся приобретают практику увязывания свойств моделируемой ситуации (среди всех рассматриваемых последовательностей обязательно есть АП) и априорных свойств математической модели (кратность единичного корня векового уравнения).
Составление подобных задач доступно даже ученикам: уравнение 3-й или 4-й степени, решение которого можно найти одним из известных способов — угадывание, поиск рационального корня, замена переменных и др., берется в качестве характеристического; затем записывается соответствующее уравнение для последовательности с НУ.
Что касается самих таких условий, то здесь возможно составление задач на параметры. В частности, задав НУ через параметры, можно потребовать монотонность/знакоположительность/знакочередование и др. свойства последовательности.

Пример 14.
Проверить, всегда ли является арифметической прогрессией последовательность, удовлетворяющая рекуррентному соотношению
Решение. Вековое уравнение биквадратное , имеющее две пары кратных корней .
Первой паре соответствуют арифметические прогрессии a_n=a₁+(n-1)d, второй — последовательности вида a_n=(-1)^n-1(a₁+(n-1)b), являющиеся как бы перемешанными двумя АП с разностями +b и -b.

Пример 15.
При рождении и наречении имени дочери родители внесли на ее имя вклад в размере 1000 рублей под 10 % годовых. В каждый день ее рожденья они пополняли вклад на 100 руб. Какую сумму получит дочь в день своего совершеннолетия?
Решение. Обозначим через a_n величину остатка по истечении n лет. Тогда a₀= 1000. Легко видеть, что .
Мы получили линейное разностное уравнение 1-го порядка с правой частью в виде константы.
Найдем решение для случая произвольных параметров . Попытаемся свести его к однородному уравнению . путем замены переменной . Подставив, получим .
Подберем q, чтоб уравнение стало однородным и определяло геометрическую прогрессию. Это несложно

. .
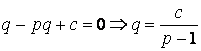
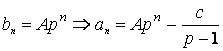Это общий вид решения. Частный случай найдем из начального условия .
Таким образом . Однако, по истечении 18-го года деньги не вносятся, а наоборот снимаются в сумме
.
Подставив a₀= 1000, p =1.10, c = 100, получим
.
Получившаяся сумма превосходит номинальную сумму вкладов 1000+100x17=2700 почти в 4 раза, причем при долгих сроках пополняемого депозита итоговая сумма в большей степени зависит от величины регулярного пополнения, чем от превосходящего его первоначального взноса.
Резюме 1: «Курочка по зернышку…» Русская народная пословица
Резюме 2: «Величайшее из изобретений человечества — сложные проценты»— барон Ротшильд.

Пример 16. Родители решили вносить на счет дочери в каждый день ее рождения число тысяч долларов, равное числу исполнившихся лет, вплоть до совершеннолетия ребенка. Какую сумму снимет дочь в день, следующий за 18-м ее днем рождения?
Решение. Обозначим a_n — остаток на вкладе на день, следующий за n-м днем рождения. Тогда .
Найдем решение по принципу «разламывания веника»: сначала для единицы — z_n, потом для n — u_n.
Первое нам уже известно: 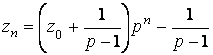, с z₀ = 0.
Второе уравнение сведем к однородному заменой .
Тогда .
Уравнение относительно w_n становится однородным, если равны свободные члены и коэффициенты при n в обоих частях:

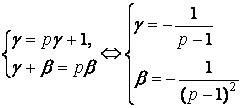
Таким образом, мы получили общее решение

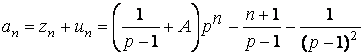
Исходя из начального условия (n=0), найдем константу A:
.
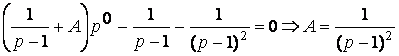
Нужное нам частное решение —
.
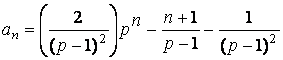Для n = 18, p=1.1 это составит тыс.$.
Очень даже неплохо — дочь становится почти миллионершей.
«Философские» замечания. Такого рода задачи решаются и методом дифференцирования суммы n+1 первых членов геометрической прогрессии (ГП) с переменным знаменателем x: S_n (x )= 1+ x+ x²…+ xⁿ.
Но, как показывает опыт автора, интерес школьников здесь гораздо ниже. Вероятнее всего, из-за «изъезженности» вдоль и поперек формулы для суммы членов ГП, скучнейших оторванных от жизни задач ради задач и т. д. и т.п.
Кроме того, мы, живя в дискретном, числовом мире, сами пропитываемся духом дискретной математики, все более сближающей математические науки и реальный мир.

Пример 17.
Инвестор заключил с компанией договор на долевое строительство квартиры стоимостью 1200 тыс. рублей. Срок строительства 1 год. Не располагая на момент заключения всей суммой, инвестор обязался уплачивать ежемесячно по 100 тыс. рублей при условии индексации долга на уровне 1 % в месяц от недоплаченной по договору суммы. Каков будет размер индексации при надлежащем исполнении им своих обязательств по договору?
Решение. Обозначим размер индексации по прошествии n месяцев со дня заключения договора как a_n.
Эта величина подчиняется следующему закону , где C= 1200 — цена квартиры, s = 0.01 — уровень индексации, при начальном условии a₀=0, так как на момент заключения договора месячный срок только начинается.
Так как вековое уравнение дает единичный корень, то общее решение этого неоднородного с линейно зависящим от n свободным членом уравнения будем искать в виде степенной суммы . Тогда для всех n (в модели не только <12) выполняется . Из выведенного нами закона следует .

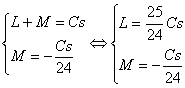
Из начального условия легко получим K = 0, и .
Для n = 12 найдем
.

Пример 18.
Семья взяла ипотечный кредит в размере 1000000 рублей сроком на 10 лет под 15 % годовых. Решили погашать равными долями. Сколько рублей они должны выплачивать ежегодно?
Решение. Аналогично примеру 13 , где p =1.15, a_n— долг банку по истечении n лет при регулярных платежах в размере c руб. Все сохраняется с разницей лишь в знаке величины c:
.
Из условий a₀=1000000, a₁₀=0 получим .

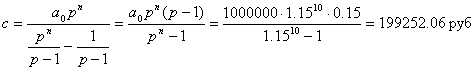
Такие вот пироги с котятами! Вынь да положь сумму без пустяка вдвое большую, а за опережения графика платежей — штраф, и не малый.
Однако, если внимательно всмотреться в формулу, легко увидеть, что при более длительных сроках ипотеки равномерный платеж мало будет отличаться от годовых процентов с одолженной суммы, и это отличие тем меньше, чем больше годовой процент.
В этом собственно и состоит математическая идея ипотеки: не можешь платить сразу всю сумму — много лет плати процент от этой суммы. В самом деле, ведь pn/(pn-1) ≈ 1. Выплачивать его придется n лет и это составит сумму S ≈n(p-1)a0. Так для 11-летнего срока она уже не 1992520.6 руб, но
.
Стоит также заметить, что равномерный платеж с соотносится с занимаемой суммой a₀ в той же пропорции, в какой pⁿ соотносится с суммой всех меньших степеней p от 0-й до (n-1)-й. И это не случайно. В финансовой математике деньги и время рассматриваются в одной связке. Так, при 10 % годовых платеж 1000 рублей 25 декабря 2007 г. — то же самое, что платеж 1100 рублей ровно год спустя, или платеж 1210 рублей спустя 2 года. И наоборот. Величина a₀pⁿ спустя n лет это то же самое, что a₀ на начальный момент. Если же поделить все платежи на p^k, k = 1, 2, 3…n — номер платежа и если их потом просуммировать, то получится все то же a_0.

Пример 19.
Семья передумала погашать равными долями. Решили увеличивать платежи с каждым годом на 10 %. Сколько составит первый взнос? Какую сумму они выплатят?
Решение. Начальный платеж c будет ежегодно возрастать в q=1.1 раз, и долг подчиняется уравнению:

.
Это также неоднородное уравнение, но «свободный член» зависит от n показательным образом.
Сведем уравнение к однородному заменой . Тогда . Нарушающие однородность члены типа Aqⁿ взаимно уничтожатся, если
.
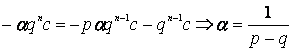Тогда .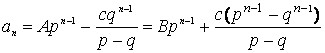
Из начального и конечного условий получим
.
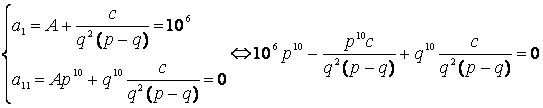Отсюда .
Общая сумма .
Замечание. Обратить внимание на знаменатель в первой формуле для решения. При p=q мы получим бесконечно большое слагаемое. Но в следующей формуле имеет место неопределенность, т. к. числитель тоже обращается в ноль. Это признак того, что вид решения меняется качественно (см. далее резонанс).

Пример 20.
Решите предыдущую задачу при прочих равных условиях, но при платежах, ежегодно возрастающих на 15 %.
Решение. Сохраним все те же обозначения. Но теперь начальный платеж c будет ежегодно возрастать в q= p=1.15 раз. Тогда получим уравнение .
Решение предыдущей задачи здесь не проходит (резонанс!). Решение получаем из формулы 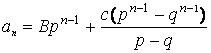путем деления числителя на знаменатель:

При p=q имеем
Из условий a₀=1000000 и a₁₁ = 0 получим
,

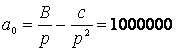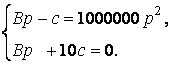
Решив эту систему линейных уравнений, найдем первый взнос 132250 рублей.
Полная же сумма составит
.
Это уже ловушка! Семья, полагая, что сэкономит средства на системе прогрессирующих платежей, сбережет лишь где-то около 120 тыс. руб в первые четыре года, но потеряет более 1200(!) тыс. руб в оставшиеся 6 лет. Эмоционально, необдуманно приняв эти условия без детального уточнения всех платежей (а человеку с улицы — не математику, не финансисту разобраться в ипотечных хитросплетениях очень сложно!), заемщики, вероятно, пожелают изменить условия договора и автоматически попадут под немалые штрафные санкции — за изменение условий, за опережающие платежи и пр. и безнадежно испортят свою кредитную историю.
Резюме. Неожиданным является даже тот факт, что первый платеж не равен 10-й части ипотечного займа, но превосходит его в квадрат мультипликатора p. А остальные будут «гораздо-еще». Это трудно предугадать при заключении договора, не решив математическую модель.

(Пример 1-10, 11-20, 21-30, 31-40, 41-55)

Содержание

вернуться на страницу Дистанционная поддержка