ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 2 Дидактический материал

Примеры 21-30  

Пример 21

После того, как море отступило от суши, в горах осталось озеро объемом V =0.1 км³ с соленой водой (MgCl) концентрации p= 20 %. Из озера вытекал ручей, ежегодно унося a= 10000 м³ воды, восполняемой осадками. Сколько лет назад закончился всемирный потоп, если в настоящее время концентрация этой соли в воде равна q = 1 %? (Считается, что горные породы вокруг не содержат магния.)

Пример 22.  (⁷, с. 198)
Сосуд содержит p%-ный раствор кислоты. Из него отлили a литров и добавили то же количество q%-ного раствора кислоты (q < p). Затем после перемешивания эту операцию повторили еще (k-1) раз, после чего получился r%-ный раствор кислоты. Найдите объем сосуда V.
Решение. Рекуррентное соотношение между концентрациями при двух последовательных разбавлениях: . То есть, мы получили «пополняемый вклад», но с отрицательными годовыми процентами . Решение такой задачи нам уже известно: .
Заменив переменные, получим
 

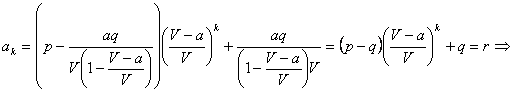
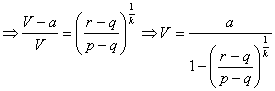
Замечание. Решение подобных практически полезных задач «в лоб» приведет к громоздкостям и неизбежным арифметическим ошибкам. Однако, если составить модель процесса в дискретном времени, найти общее решение, а по начальным условиям — частное, то мы сразу получим верный ответ. Проанализировав его, можно сделать ряд полезных качественных и порой неожиданных выводов (см. выше).

Пример 23.
В некотором государстве s =1/3 годового валового продукта (ВП) расходуются на инвестиции в экономику в следующем году, а эффект от них проявляется еще через год. При этом известно, что прирост валового продукта пропорционален вложенным инвестициям с коэффициентом p=4/3 (>1). Составьте уравнение, определяющее эволюцию ВП, и решите его, если известно, что в первые два года ВП не изменялся и равнялся единице.
Решение.

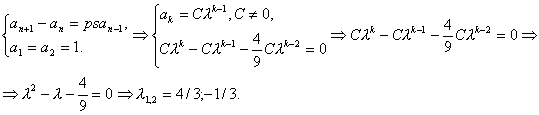
— общее решение.
Частное решение находится из начальных условий:

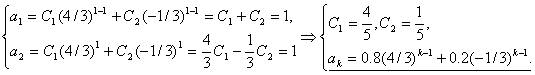
Методические замечания. Эта стандартная линейная модель влияния инвестиций на прирост ВП при решении дает всегда сумму двух геометрических прогрессий: одну возрастающую, другую — знакопеременную. В нашем случае эта вторая — бесконечно убывающая, и из-за малого ее весового множителя (0.2) и малого знаменателя (|q|=1/3) сумма будет монотонно расти с номером k. Но, при , т. е. ps>2, мы получим знакочередующуюся возрастающую по модулю прогрессию. Возможно ли при некоторых допустимых НУ частное решение, немонотонное при k>2?
Этот дискуссионный вопрос, вероятно, разобьет аудиторию на «абстрактных математиков» и «реалистов». Первые попытаются привести такой пример подбором начальных условий; вторые же скажут: «Убывание не предусмотрено самой моделью a priori, т. к. прирост ВП всегда положителен, ведь отрицательными инвестиции быть не могут». И это будет еще одним важным опытом анализа модели без ее детального решения.

Пример 24.
а) Выведите формулу для суммы квадратов первых n натуральных чисел через решение разностного уравнения; б) найдите сумму всех попарных произведений различных натуральных чисел от 1 до n.
Методические указания. а) После того, как сумма членов АП будет найдена как решение разностного уравнения , учащиеся сделают вывод, что суммирование линейных по номеру выражений приводит к квадратичному по максимальному номеру. Тогда сам собой напрашивается метод неопределенных коэффициентов (МНК):
.
Коэффициенты можно найти «в лоб», взяв N =1,2,3,4. Но получится система из 4-х линейных уравнений, решение которой — трата времени. Если не «в лоб», то необходимо вернуться к исходному разностному уравнению, но с «известными» S_N⁽²⁾
.
Приравнивая коэффициенты при различных степенях N, легко найдем последовательно d(=1/3),c=1/2 и b=1/6; из начального условия S₁⁽²⁾=1 найдем A =0.
Разбирая этот и аналогичные примеры, учитель вооружает учащихся еще одним методом вычисления определенных интегралов от степенных функций, избегая тем самым неочевидной формулы Ньютона— Лейбница, вводимой в учебных комплектах на нестрогом, наглядном уровне.
б) Задача скорее олимпиадная, предполагает креативность мышления и направлена на развитие ее. Школьник должен сообразить, из каких выражений можно сконструировать такую сумму. Поэтому «опускающей» уровень подсказкой здесь будет формула (1+2+3+…+N)2=… .

Пример 25.
В сборнике тренировочных заданий для подготовки к ЕГЭ (⁶, с. 45) приведена следующая задача.
«В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала повышать сотруднику зарплату на 3 %. Однако в связи с финансовыми затруднениями она смогла повышать зарплату только раз в полгода (в начале следующего полугодия). На сколько процентов фирма должна повышать зарплату каждые полгода, чтобы 1 января следующего года зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренной (предусмотренным?- мой) договором.»
Решите эту задачу для годовой зарплаты, т.е. суммы всех месячных зарплат:
а) без учета возможности размещения недоплачиваемых сумм на депозит из расчета 2 % в квартал;
б) с таким учетом.

Пример 26.
Выполните действия над матрицам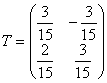и , и :
а) ST; б) TS; в) (TA)S; г) T(AS); д) S(AT); е) A2.
Решение. а), б) это так называемые взаимообратные матрицы S=T^-1 и T = S^-1. В самом деле

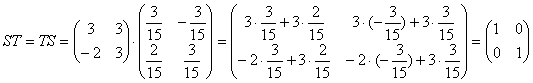
Получили т.н. единичную матрицу , при умножении которой на любую возможную матрицу ее же и получаем. Также, при умножении этой матрицы на любой геометрический вектор результат не изменяется.
Она (E) — как бы нулевая степень матрицы S (и T, и любой другой невырожденной матрицы, т. е. для которой существует обратная). А T =S^-1 — минус-первая степень квадратной невырожденной матрицы S.
Таким образом, квадратную невырожденную матрицу можно возводить в любую целую степень, при этом сохраняются все свойства степеней. Более того, из матриц можно даже извлекать квадратные и пр. корни, но только их будет бесконечно много.
Из матриц можно формировать матричные последовательности, аналогичные числовым, например, E, A, A², A³ и т. д. И они также могут иметь предел, тоже матрицу. То есть по мере возрастания номера члена последовательности, все его элементы практически перестают изменяться и каждый стремится к своему предельному значению.
Так доказывается, что для любой матрицы A (kxk) существует предел матричной последовательности , называемой экспонентой матрицы A: . Эта предельная матрица всегда имеет обратную, т. е. невырождена, и она равна e^-A=exp(-A).
Аналогичным образом определяется матричная показательная функция Y(t)=exp(tA). Так же, как и для числовой экспоненты, для нее справедливо (нетрудно показать см. пример № 8) разложение в бесконечную сумму (ряд) .

Как и для числовой экспоненты, производная по t

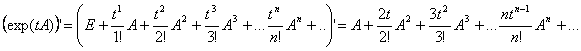
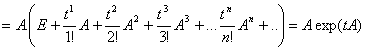
Сохраняются и все остальные свойства экспоненты, в частности, интеграл

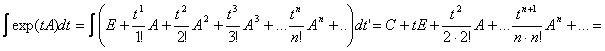
Последнее — верно лишь для невырожденных матриц A, и проверяется простым дифференцированием.
Пример экспоненты должен навести учащихся на мысль о существовании любых функций от матриц: многочленов, тригонометрических, радикалов и т. д. и о выполнимости на таких функциях всех правил дифференцирования и интегрирования, и др. элементов математического анализа. Проблема заключается в том, как вычислять значения таких функций. Пункт ниже показывает один из путей решения такой задачи.
в) Получается — т. н. диагональная матрица. Такие матрицы тем хороши, что при возведении их в любую степень .

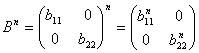
Замечание. Учащиеся профильных классов знают о разложении элементарных функций в ряд Тейлора. (Даже в непрофильных изучают разложение в ряд для |x|<1
y(x) = 1/(1-x)=1+x+x²+…). Используя эти разложения, можно вычислять функции от матриц. От диагональных матриц такие функции вычисляются просто —

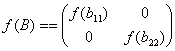
Как вычисляются функции от произвольных матриц, показывает пример ниже.

Пример 27. (Представляется в виде компьютерной презентации с проверкой учащимися правильности вычислений)
Найдите A²⁰ из предыдущего примера с использованием калькулятора.
Решение. Вычислить матрицу можно двумя путями.
1) Разложим по степеням двойки 20=16 +4=2⁴+2². Тогда A20=(A²)²+ ((A²)²)². Тогда




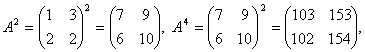
Возникли громоздкие вычисления, и это только для частного случая двадцатой степени! Необходимо искать другой путь.

2) По свойству ассоциативности умножения матриц (сочетательный закон)


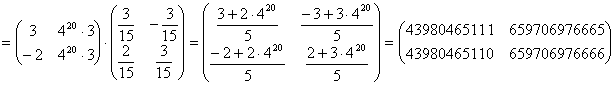
(И для 20-й степени элементы в столбцах отличаются на единицу! Попробуйте сформулировать гипотезу о матрицах типа и проверить доказательством по индукции, что это верно для всех степеней.)
Таким образом, если нам известны взаимообратные функции S и S^-1, которые умножаясь слева-справа на исходную матрицу приводят ее к диагональному виду B, то проблема вычисления функции F(A) от матрицы решена: точно так же, как мы нашли

P(A) = A²⁰. Найдем любую степень в разложении в ряд, осуществим суммирование и предельный переход. Получим F(A)=SF (B)S^-1. А что касается нахождения матриц S и S^-1, то это возможно не для любой матрицы A, и в настоящем предмете данный материал не рассматривается. Интересующиеся учащиеся могут ознакомиться на информационном уровне с этим материалом самостоятельно.

Пример 28.
Умножьте матрицу на геометрические векторы а) b₁=(3;-2), б) b₂=(3;3), в) 2b₁, г) -3b₂, д) 2b₁-3b₂.
Методические указания. Пп. а, б) Векторы b₁-и b₂ — суть неколлинеарные собственные векторы для матрицы A. Умножаясь на нее, они дают результат, коллинеарный исходному продукту. Коэффициенты пропорциональности при этом равны -1 и 4 — собственные числа матрицы A.
Пп. в,г). Этих векторов бесконечно много, т. к. умножая любой из них на действительное число, мы также получаем собственный вектор.
д) Любой вектор плоскости, представленный в виде разложения по собственным — в базисе собственных векторов, умножаясь на матрицу A, меняет на противоположную свою первую координату:2→ -2 и удлиняет в 4 раза свою вторую координату: -3→ -12. Такое преобразование, будучи примененным ко всем векторам плоскости (радиус-векторам всех тт. плоскости), является комбинацией гиперболического поворота и отражения.
Если бы оба собственных числа были положительными, то мы имели бы такой поворот в чистом виде. Эти повороты хорошо представлены в научно-популярной литературе для школьников на примере растягивающихся/сужающихся «кошачих мордочек» и т. п. Интересно, что вращаясь гиперболически, мордочка никогда не покинет свою родную «координатную четверть», но при этом вытянется, либо сплющится в зависимости от того больше собственное число единицы, либо между нулем и единицей.
Школьники должны обратить внимание на то, что столбцы одной из взаимообратных матриц, при помощи которых диагонализируется A к виду B, — суть координаты собственных векторов. После диагонализации A — на главной диагонали находятся собственные числа.

Пример 29. ( Матрица поворота)
Умножьте матрицу на векторы а) e₁=(1;0) и e₂=(0;1); б) x =(x₁;x₂) . Изобразите результат на плоскости для φ=p, p/2, p/4 и p/6.
Замечание. Это — матрица поворота на угол φ, т. к. будучи умножена на любой вектор плоскости, переводит его в вектор, повернутый относительно исходного положения на такой угол против часовой стрелки. Для развернутого угла это также матрица инверсии на плоскости. Для любого положительного числа M матрица MA_φ есть поворот и растяжение/сжатие в M раз. (См. далее комплексные числа).
У такого рода матриц (кроме случаев φ=±p) не может быть собственных векторов с действительными координатами. Но зато есть такие векторы с комплексными координатами, т. е. все те же матрицы специального типа.

Пример 30.
На множестве матриц решите уравнение .
.
Указание. Решение возможно через систему двух нелинейных уравнений; ответ желательно представить в виде комбинации двух матриц — диагональной и антисимметричной.
Решение. Ищем корни этого уравнения в виде . Тогда

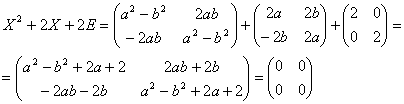
Получим систему уравнений
.
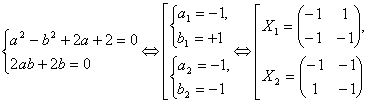
Обратите внимание на то, что случай b = 0 не дает действительных решений. Но если мы разрешим величинам a и b принимать комплексные значения, то будет еще пара корней, представимых уже в виде блочных действительных матриц 4x4. Таким матрицам соответствуют т. н. гиперкомплексные числа или кватернионы, широко используемые в различных разделах физики и механики, в особенности для описания изменения разного рода математических величин при пространственных поворотах.
 

(Пример 1-10, 11-20, 21-30, 31-40, 41-55)

Содержание

вернуться на страницу Дистанционная поддержка