ДИСТАНЦИОННАЯ ПОДДЕРЖКА
учителей математики

Чистяков В.В
к.ф.-м.н.,
доцент кафедры ЕМД

Приложение 2 Дидактический материал

Примеры 41-55  

Пример 41
Материальная точка начинает двигаться по прямой из начала координат вправо со скоростью v₀=1, при этом ее ускорение пропорционально корню квадратному из модуля скорости с коэффициентом k =1, но направлено а) по скорости; б)* против скорости, т. е. действует сила сопротивления. Найдите законы движения точки в обоих случаях. Как далеко уйдет от начала координат вправо точка в случае б)? Остановится ли она?
Указание. Помимо стандартного пути решения через свойства семейств линий составленное нелинейное дифференциальное уравнение можно свести к неполному заменой .
Решение. После замены уравнение движения примет вид . Тождественно равное нулю решение y(t) = 0 не удовлетворяет начальному условию (NB!). Тогда
.
Ускорение . Чтобы оно было направлено по скорости в нулевой момент, необходимо, чтоб C>0. Для случая б) наоборот C<0. Тогда в случае а) C=1; в случае б) C=-1. Соответственно, законы движения суть .
Что касается случая а), то здесь материальная точка неограниченно удаляется вправо с возрастающей по квадратичному закону скоростью.
Другая ситуация в случае б). До момента t = 2 с точка движется вправо, но затем, развернувшись, неограниченно удаляется влево. Модель дает неверное решение?
Нет, верное только до определенного момента: точка останавливается через 2 секунды, пройдя 1/3 метра, и продолжает стоять вечно. Она не развернется, и есть два объяснения этому.
Физическое: чтобы сдвинуться хотя бы на микрон влево, необходимо совершить работу против сил трения, а для этого необходима кинетическая энергия, которой нет в точке остановки.
Математическое (от противного): при движении влево скорость как алгебраическая величина стала бы отрицательной, т. е. убыла. Но при этом ее производная — ускорение было положительно. Таким образом, у нас нарушается достаточный признак возрастания функции. Но, ничто не нарушено, если v(t) = 0 при t>2.
Следовательно, выведенный закон б) верен лишь для t≤2 c. Для бòльших времен x(t)=const =1/3 м, и мы получили конечные тормозные время и путь..
Решение примера, во-первых, показывает, казалось бы, очевидную невозможность возвратного движения в системе, где сила являет собой только сопротивление движению. (Причем это верно для любого показателя степени, не только для квадратного корня, вообще для любой зависимости силы от v). Однако чисто формальный подход к оценке полученного результата дает немыслимое поведение.
Во-вторых, он дает возможность школьникам, проанализировав, сделать вывод о том, что время и путь торможения конечны лишь тогда, когда сила сопротивления зависит от скорости по закону, сильнее, чем линейный вблизи v=0. Школьник видит, к чему приводит зеркальность степенного поведения вблизи нуля и на бесконечности.
В-третьих, школьники, решая, получают на ступеньку (или на «степеньку») более высокий, кубический закон движения x(t), и видят, что в обоих случаях он обеспечен именно корневой зависимостью ускоряющей силы от скорости. Поделенная на 3 третья производная при этом — отличная от нуля константа, и она называется темпом ускорения.
Наконец, в-четвертых, школьники на наглядном уровне, нестрого, но узнают, что если в уравнении динамики (изменения) величины присутствует корень (любой степени) или модуль искомой величины, то нарушается закон единственности частного решения при заданных начальных условиях. Как и в алгебре, корни и модули здесь враги единственности. В момент, когда величина достигает нулевого значения, возникает раздвоение поведения системы.

Пример 42. (Анализ результатов модели)
Шофер, двигаясь со скоростью v= 72 км/ч, затормозил за 40 м до поста ГИБДД и двигался с отрицательным ускорением a = -5 м/c². Через какое время он поравняется с постом?
Ответ: 4 с.
Замечание. Составление и решение квадратного уравнения дает два, казалось бы, равноправных положительных корня. Но глагол «затормозил» исключает больший.

Пример 43. (Анализ готовых моделей)
Заяц находится в начале координат, волк на оси абсцисс в т. W(1;0). Одновременно заметив друг друга, заяц начинает убегать по оси Oy в положительном направлении, а волк бежит так, что его скорость в любой момент времени направлена на зайца и по величине равна скорости зайца. Известно, что среди 5-ти функций ниже имеется функция, описывающая траекторию волка (пунктир, рис. 2) в выбранной системе координат. Определите ее и обоснуйте выбор.
а) 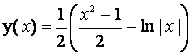; б) ;
в) ; г) ;
д)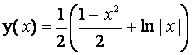
.
Рис.2.
Решение. В начальный момент ордината волка равна 0, абсцисса единице. Проходят все пять моделей.
Вектор скорости волка в тот же момент направлен к началу координат, т. е. касательная к траектории в исходной точке горизонтальна. Поэтому, п. б) исключается.
Далее, очевидно, волк никогда не догонит зайца— ведь их мгновенные скорости в любой момент равны по величине, временные интервалы движения одинаковы. Следовательно, должны быть равны и пройденные («пробежанные») расстояния. Их «встреча» возможна только на оси ординат. Тогда проекция криволинейной траектории волка окажется равной по длине самой кривой.
Это, понятно, невозможно, следовательно «встречи» не будет, и значение x=0 не войдет в область определения D(y). Поэтому, исключается п. в).
Остаются пп. а, г и д). Но в п. д) волк бежит вниз от зайца, и его скорость никак не может быть направлена к последнему. Таким образом, остаются пп. а) и г).
Они удовлетворяют вроде бы всем изначально ясным требованиям реальной ситуации. А та обладает очевидной симметрией: если б волк изначально находился в точке W’(-1;0), симметричной относительно оси ординат, то траектория преследования также была бы симметрична исходной. То есть y(x) — четная функция (поэтому в логарифме модуль!). Но только в п. а) функция является четной.

Методические замечания. Задача целиком и полностью на развитие аналитического и критического мышления, а также на чрезвычайно важное понятие математической логики — «импликацию». Из реальной ситуации школьник должен уметь вычленить все характерные особенности, моменты процесса. Далее готовые модели анализируются, тестируются на соблюдение этих моментов. Если хотя бы один момент, один априорный факт не объясняется моделью, она отвергается.
Но стоит подчеркнуть учащимся, что даже выполнение всех зафиксированных моментов в анализируемой модели еще не есть гарантия ее правильности, адекватности. Здесь реализована логическая операция «импликация», выражающая необходимые условия для реализации некоторого явления. «Ружье выстрелило — значит, курок был нажат»— так можно наглядно объяснить ученикам «импликацию». Но даже, когда нажимают курок, ружье не всегда стреляет — случаются осечки. Здесь «нажатым курком» являются начальные условия (положение волка, касание траекторией оси абсцисс) и т.н. асимптотическое поведение траектории, а именно, наличие правосторонней вертикальной асимптоты. «Выстрелом» здесь является правильность уравнения траектории серого.
Коль верная формула дается свыше, то имеет смысл обсудить с учащимися, какие соображения— аналитические соотношения, м. б. графические образы легли в ее основу. В рамках программы углубленного изучения возможно составление дифференциального уравнения траектории, а вот решение — уже вузовский материал.

Пример 44. (Обратная функция)
Волк находится в точке V(0;1), заяц в начале координат и убегает по оси Ox. Запишите уравнение траектории волка.
Ответ: .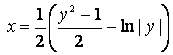

Пример 45. (Анализ готовых моделей)
В примере 43 скорость волка превышает в любой момент скорость зайца в k>1 раз. 1) Установите соответствие между случаями k =2, 3 и 4 и пп. а), б) и в). 2) Постарайтесь угадать формулу траектории волка для произвольного k>0, отличного от 1.
а) ; б) ; в)
Ответ: 1)
k= 2 3 4
п. а в б
Указание: Чем больше скорость волка, тем меньше пробежит заяц по оси ординат, прежде чем его схватит волк (x=0).

2) .
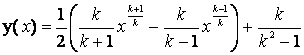Замечание. В силу аналитических свойств выведенного (не нами!) через решение дифференциального уравнения функции y(x) формула будет верна и тогда, когда волк бежит медленнее зайца, т. е. при 0 < k < 1.
Но неопределенность возникает при k=1, и здесь решение имеет качественно иной вид. Наряду с сохраняющимся старшим степенным слагаемым, младшее слагаемое преобразуется в трансцендентное ln/x/. И мы можем утверждать, что при k→1, k>1
,
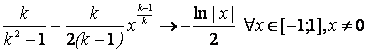при этом, не вторгаясь в область вузовской (т.н. высшей (?)) математики.
Но будет ли формула верна при отрицательных k? То есть, когда волк разбегается с зайцем. Естественно, он будет бежать в IV-й четверти «вниз». Оказывается, и тогда модель верно описывает траекторию, но при этом особый случай k= -1.
Это можно показать простой заменой k→-k в формуле ответа. При такой замене y(x) →- y(x). И это не случайно. Если заснять процесс погони сверху на видеопленку с бесконечно высокой частотой кадров, и на каждом кадре изображение волка центрально отразить (инвертировать) относительно т. W(0;1), то после такой «цифровой обработки» мы получим ситуацию разбегающихся зверей.

Пример 46. (Частный случай модели)
Составьте уравнение траектории волка, разбегающегося с зайцем, для случая k = -1/2, исследуйте и постройте на миллиметровой бумаге в масштабе по точкам на отрезке [1;2]. При помощи нити экспериментально определите длину этого отрезка линии и сравните с теоретической.
Ответ. .
Указание. Эту работу также можно выполнить с использованием компьютерной программы, предназначенной для построения и исследования графиков. Поэтому весь мини-проект «волк— заяц» можно осуществить с использованием ИКТ.

Пример 47 (Работа с готовой моделью, извлечение математических фактов)
Определите, как зависит от абсциссы положения волка x расстояние между волком и зайцем в Примере 42. Особое внимание уделите поведению этой величины при неограниченном возрастании пути погони.
Решение. Решаем задачу в общем случае. Как зависит от абсциссы точки касания x₀ к кривой y(x)= f(x) расстояние от этой точки до точки пересечения касательной с осью ординат.
Уравнение касательной к кривой в точке x₀ имеет вид
.
Точка пересечения с осью ординат —A(0; y_кас(0)),т. е. .
Разности ординат и абсцисс для рассматриваемых точек
.
Расстояние равно .
В нашем случае .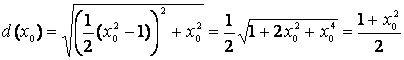
Нетрудно видеть, что оно уменьшается по мере погони от d₀ =1 и стремится к постоянной величине d_∞ = 0.5 при неограниченном удалении зверей от начала координат.
Пример иллюстрирует понятие предела и асимптоты в «живом», неформальном разрезе. Школьник убеждается, что если некоторый график имеет вертикальную асимптоту, то его длина от фиксированной точки до точки, отдаляющейся на бесконечность, отличается от длины проекции на асимптоту на все более постоянную положительную величину. Причем это верно для любых асимптот: наклонных, горизонтальных, вертикальных.
А обратно? Можем ли мы утверждать, что если разность между путем по неограниченному графику Г(f(x)) и проекцией этого пути на некоторую прямую l , для определенности — слева от графика, стремится к постоянной величине, то у этого графика имеется асимптота, параллельная прямой l ? Такую проблему можно выдать для самостоятельного исследования дома.
Доказательство для вертикальных асимптот почти простое, и оно строится на детском приеме меряться затылками: кто выше. Через начальную точку графика A проводится прямая h _┴ l . Из точки графика M₁(x,y) «вдали от…» опускается перпендикуляр l₁ на h. Длина l₁ равна проекции участка графика AM на l. Выбирается т. M₂(x,y) далее по графику, т. е. L(AM₂) > L(AM₁). Снова опускается перпендикуляр l₂ на h, равный по длине проекции участка AM₂, и так до бесконечности. Мы получим последовательность параллельных отрезков { l_n}, сдвигающихся в одном направлении, но не переходящих некоторую границу l. Длины их неограниченно возрастают, т. к. от соответствующих длин участков графика отличаются на ограниченную величину. Длины путей на графике стремятся в бесконечность, ведь график не ограничен. Тогда последовательность длин перпендикуляров тоже стремится в бесконечность, следовательно, отрезки в пределе дают луч, параллельный l. Это и будет асимптота.

Пример 48. (Маятник без затухания, формула Эйлера)
Найдите либо подберите из известных вам элементарных функций общий вид y(t) решений однородного линейного ДУ . Ответьте на вопросы:
1) Каким образом здесь можно избежать введения комплексных чисел в вековом уравнении?
2) Если y₀(t) — частное решение уравнения, то будет ли таковым z(t)= y₀(t+C), C — любое действительное число?
Решение. Решение векового уравнения дает комплексные корни λ_1,2=±iω, причем чисто мнимые, что является прямым указанием на периодичность решения. Однако реальное смещение маятника является действительной величиной. Следовательно, из комплексных выражений e^±iωt, или удобнее exp(±iωt), существующих лишь в нашем воображении, можно, используя свойства линейности решаемого уравнения, сконструировать действительные величины: exp(+iωt)+ exp(-iωt)= 2cosωt либо –i{exp(+iωt)- exp(-iωt)}= 2sinωt. А уже из них — y(t)= Asinωt + Bcosωt.
Это пример, как и в случае анти-фибоначчиевых чисел, демонстрирует полезность экскурса в область реально несуществующих величин (комплексных чисел, т. е. количеств) при моделировании вполне реальной физической системы.
Комплексных чисел можно избежать переходом от уравнения II-го порядка к системе уравнений I-го:
.
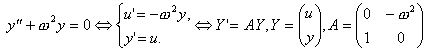Матричный вид системы дает универсальным образом решение (проверьте!).
При определении матричной экспоненты e^tA мы легко найдем

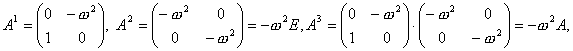
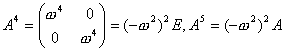и т. д.
Суммируя порознь четные и нечетные степени и учитывая временной множитель t, получим
.
Любопытно, что при w=1 мы получаем матрицу поворота на угол t рад.

Пример 49.
Решите это уравнение с начальными условиями (задача Коши)
.
Проанализируйте частные случаи A=0, B≠0 и наоборот B=0, A≠0.

Пример 50. (Резонанс)
Подберите и проанализируйте решение неоднородного линейного ДУ
.
Решение. Поиск частного решения в виде y=Asin(cos)ωt приводит к неверному равенству 0=sin(cos)t для всех действительных t. Функции вида tg(ctg)t не удовлетворяют из-за различия в областях определения левой и правой частей.
Мы знаем, что производная от произведения синуса (косинуса) на многочлен представляется в виде комбинации подобных выражений. В самом деле (tsinωt)’= sinωt+ωtcosωt, (tsinωt)’’= ωcosωt+ωcosωt- ω²tsint=2ωcosωt- ω²tsint.
Тогда левая часть — (tsinωt)’’+ ω²tsint=2ωcosωt, т. е. она пропорциональна правой части ДУ. Для верного равенства необходимо поделить на 2ω. Получим
Это — частное решения. Для получения общего необходимо добавить решение однородного ДУ — Asinωt + Bcosωt.
Как велики ни были бы A и B выражение Asinωt + Bcosωt ограничено по модулю (какова точная верхняя граница?). Что же касается частного решения y₀(t), то оно неограниченно по абсолютной величине, и его график соответствует линейно возрастающим по амплитуде колебаниям. В механике, физике такое решение описывает явление резонанса, возникающее, когда совпадают частоты вынуждающей силы и собственных колебаний маятника, колебательного контура, конструкции и т. п.
Именно на явлении резонанса работает радио- и мобильная связь, позволяющая при малой мощности передатчика передавать сигнал на отдаленную вышку.

Пример 51. (Маятник с сопротивлением, презентация)
На пружинный маятник массы m с круговой частотой собственных колебаний ω0 начала действовать сила сопротивления со стороны среды F_сопр..= -fv.
1) Составьте уравнение и найдите закон движения, если а) начальное положение x₀ = 0, v₀>0 — начальная скорость; б) x₀= x_max=A, v₀=0. Рассмотрите все возможные случаи и постройте эскизы графиков.
2) Остановится ли маятник когда-либо во всех этих случаях? Найдите пределы длин путей, пройденных маятником.
Замечание. Задача дается на дом как самостоятельное исследование, но разбирается в классе с использованием компьютерного продукта «Открытая физика», тема «Колебания» и оформляется как презентация (можно путем сканирования). Учителя математики не должно смущать механическое содержание проекта, т. к. механика и математика часто трудноразделимы. (Иначе Софья Ковалевская — не великий русский математик, но механик. Ведь основное ее научное достижение относится к динамике вращающегося твердого тела.)
В этой задаче в зависимости от знака дискриминанта характеристического уравнения получают: затухающие колебания при комплексных корнях, критическое затухание при кратном корне и закритическое затухание при действительных корнях. Последние два типа относятся к апериодическому затуханию.

Пример 52. (Электромеханические аналоги)
Постройте электрический аналог маятника из предыдущей задачи и охарактеризуйте возможные процессы в цепи.
Указание. Это колебательный контур с сопротивлением. Подробный материал можно найти в любом элементарном учебнике электротехнике, но лучше в программном продукте фирмы Физикон.

Пример 53. (Биологическое равновесие в системе «хищник— жертва», предельный цикл)
В некотором ареале обитают только рыси и зайцы. Многолетними наблюдениями установлено, что среднегодовые численности обоих видов не меняются, однако на протяжении года имеют место отклонения численностей от среднегодовых величин, т. е. наблюдается избыток/недостаток. Темп прироста избытка рысей пропорционален избытку зайцев. Темп убыли избытка зайцев пропорционален избытку рысей. Введите переменные и необходимые параметры и составьте модель эволюции во времени для численностей этих двух популяций. Сможете ли вы решить, найти в научной литературе, интернете и т. д. решение этой задачи. Как выглядит на координатной плоскости, по осям которой отложены одновременные численности этих популяций, т. н. «портрет» этого решения.
Замечание. Пример чисто ознакомительного характера, демонстрирующий эффективность математического моделирования даже в зоологии. Подробно учитель может взять материал из монографии В.И. Арнольда¹⁵. Пример поучителен даже с философской точки зрения, не только экологической.

Пример 54. (биржа)
Котировка акции на бирже (ММВБ, РТС и др.) определяется балансом спроса и предложения. Если они уравновешены, то курс бумаги с хорошей точностью можно считать неизменным (случайные колебания, «шум»). Котировка растет, если спрос на актив превышает предложение, и падает, если наоборот. Пусть спрос на актив зависит от цены p по линейному закону D(p)=k(a-p), k>0 и он падает с ростом цены. Предложение наоборот растет с ценой: S(p)=q(p-b). Составьте модель изменения котировки p(t) в предположении, что мгновенная скорость ее изменения пропорциональна с коэффициентом α (ценовой подстройки) дисбалансу спроса и предложения. Исследуйте поведение решения при t→+∞.
Указание.

Пример 55. (снова биржа— мини-исследование)
Проанализируйте поведение котировки p(t) для следующих функциях спроса и предложения:

при различных начальных условиях p(0) = p₀.
Указание. В этой модели продавцы и покупатели разделены, т. к. спрос и предложение не переходят друг в друга, становясь отрицательными. Как только цена p оказывается выше a, спрос выключается, и работает только предложение, при p < b отключается предложение. Поведение цены вблизи границ интервала (a;b) более плавное, т. е. котировка более долгое время может быть вблизи этих границ, но потом все равно будет стремиться к равновесному значению. Однако, на протяжении дневной торговой сессии величины близки друг к другу, и при этом всегда есть неучтенные моделью внешние воздействия, выводящие систему из равновесия.
Решая эту задачу, школьники учатся «сшивать» разные решения в общем виде и таким образом получать непрерывную кусочно-показательную функцию, присутствующую в школьном курсе без всякой связи с другим материалом, но только ради исследования на непрерывность.
 

(Пример 1-10, 11-20, 21-30, 31-40, 41-55)

Содержание

вернуться на страницу Дистанционная поддержка