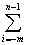| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Системы счисления. | |
|
1 |
Запустить программу Системы счисления (файл system.exe ) | |
|
2 |
Ввести команду [Системы-Единичная]. | |
|
3 |
В появившемся диалоговом окне Единичная система ознакомиться с содержанием текстовых окон История системы и Сущность системы, а в окне Калькулятор набрать какое-либо число. |
|
Единичная система — не самый удобный способ записи чисел. Записывать таким образом большие количества утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные, системы счисления.
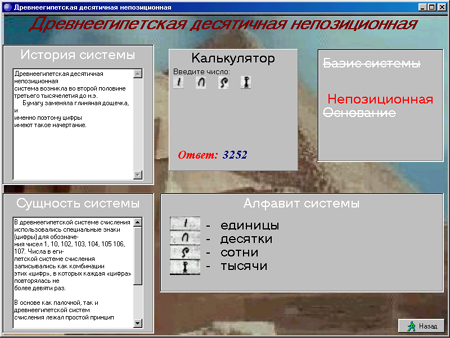
Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.
|
! |
В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа. |
Например, чтобы изобразить 3252 рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы). Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемежку.
|
4 |
Ввести команду [Системы-Древнеегипетская]. | |
|
5 |
В появившемся диалоговом окне Древнеегипетская система ознакомиться с содержанием текстовых окон История системы и Сущность системы, а в окне Калькулятор набрать число, например, 3252. |
|
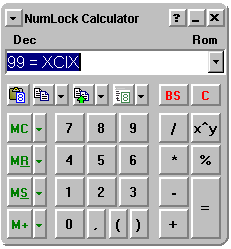
Римская система счисления. Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (Сentum — сто, Demimille — половина тысячи, Мille — тысяча).
Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII=10+10+5+1+1+1 (два десятка, пяток, три единицы).
Для записи промежуточных чисел римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Например, IX — обозначает 9, XI — обозначает 11.
Десятичное число 99 имеет следующее представление:
XCIХ = -10+100-1+10.
|
6 |
Запустить программу NumLock Calculator. | |
|
7 |
Ввести команду [Формат результата-Римский]. | |
|
8 |
В окне ввода данных ввести число, например, 99, и нажать клавишу со знаком «=». Появится результат, число, записанное в римской системе счисления.
|
|
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется, в основном, для наименования знаменательных дат, томов, разделов и глав в книгах.
Алфавитные системы счисления. Более совершенными непозиционными системами счисления были алфавитные системы. К числу таких систем счисления относились греческая, славянская, финикийская и другие. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 100 до 900) обозначались буквами алфавита.
В алфавитной системе счисления Древней Греции числа 1, 2, ..., 9 обозначались первыми девятью буквами греческого алфавита, например a = 1, b = 2, g = 3 и т.д. Для обозначения чисел 10, 20, ..., 90 применялись следующие 9 букв (i = 10, k = 20, l = 30, m = 40 и т.д.), а для обозначения чисел 100, 200, ..., 900 — последние 9 букв (r = 100, s = 200, t = 300 и т.д.). Например, число 141 обозначалось rma.
| У славянских народов числовые значения букв установились в порядке славянского алфавита, который использовал сначала глаголицу, а затем кириллицу. Подробнее с происхождением и развитием русской письменности можно ознакомиться на сайте «История русской письменности», размещенном на нашем CD-ROM. | 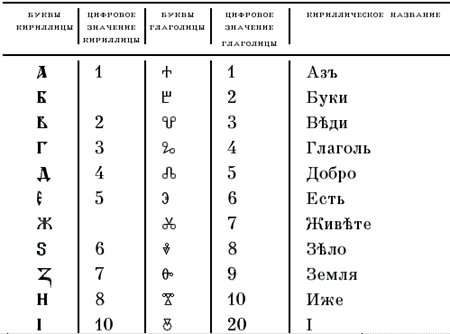
Рис. 2.2. Древнерусская алфавитная система счисления |
В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранилась только в богослужебных книгах.
Непозиционные системы счисления имеют ряд существенных недостатков:
1. Существует постоянная потребность введения новых знаков для записи больших чисел.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.
2.2.2. Позиционные системы счисления
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.
Основанием позиционной системы счисления называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию.
Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число не меньшее 2. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и т. д.).
|
! |
В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа. |
Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степени числа 10.
В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q, иначе говоря, q единиц какого-либо разряда образуют единицу следующего разряда. Для записи чисел в q-ичной системе счисления требуется q различных цифр (0,1,...,q-1).
В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем виде:
|
2.4 |
Аq= ± (an-1qn-1+an-2qn-2+...+a0q0+a-1q-1+a-2q-2+...+a-mq-m) |
или
|
2.5 |
Аq = ± |
Здесь А — само число,
q — основание системы счисления,
ai —цифры, принадлежащие алфавиту данной системы счисления,
n — число целых разрядов числа,
m — число дробных разрядов числа.
Свернутой формой записи числа называется запись в виде
|
2.6 |
A=an-1an-2...a1a0,a-1...a-m |
Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Пример 2.7. Десятичное число А10=4718,63 в развернутой форме запишется так:
А10=4·103+7·102+1·101+8·100+6·10-1+3·10-2
Пример 2.8. Двоичная система счисления.
В двоичной системе счисления основание q=2. В этом случае формула (2.4) принимает вид:
А2= ± (an-12n-1+an-22n-2+...+a020+a-12-1+a-22-2+...+a-m2-m)
Здесь аi — возможные цифры (0, 1).
Итак, двоичное число представляет собой цепочку из нулей и единиц. При этом оно имеет достаточно большое число разрядов. Быстрый рост числа разрядов — самый существенный недостаток двоичной системы счисления.
Записав двоичное число А2=1001,1 в развернутом виде и произведя вычисления, получим это число, выраженное в десятичной системе счисления:
А2=1·23+0·22+0·21+1·20+1·2-1 = 8+1+0,5 = 9,510.
Пример 2.9. Восьмеричная система счисления.
Основание: q=8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Записав восьмеричное число А8=7764,1 в развернутом виде и произведя вычисления, получим это число, выраженное в десятичной системе счисления:
А8=7·83+7·82+6·81+4·80+1·8-1 = 3584 + 448 + 48 + 4 + 0,125 = 4084,12510
Пример 2.10. Шестнадцатеричная система счисления.
Основание: q=16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,1, …9. Для записи остальных цифр (10, 11, 12, 13, 14 и 15) обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3АF16 означает:
3АF16 = 3·162+10·161+15·160 = 768+160+15 = 94310.
Пример 2.11. Запишем начало натурального ряда чисел в десятичной и двоичной системах счисления:
|
А10 |
А2 |
А10 |
А2 |
|
0 1 2 3 4 5 6 7 |
0 1 10 11 100 101 110 111 |
8 9 10 11 12 13 14 15 |
1000 1001 1010 1011 1100 1101 1110 1111
|
Задания для самостоятельного выполнения (Ответы)
2.12. Какой числовой эквивалент имеет цифра 6 в числах:
|
6789 |
3650 |
16 |
69 |
2.13. Сравните числа III и 111, записанные в римской и десятичной системах счисления..
2.14. Какие числа записаны римскими цифрами:
а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?
2.15. Запишите год, месяц и число своего рождения c помощью римских цифр.
2.16. Некоторые римские цифры легко изобразить, используя палочки или спички. Ниже написано несколько неверных равенств. Как можно получить из них верные равенства, если разрешается переложить с одного места на другое только одну спичку (палочку)?
VII - V=XI IX-V=VI
VI - IX=III VIII - III=X
2.17. Заполните следующую таблицу:
|
Система счисления |
Основание |
Цифры |
|
шестнадцатеричная |
16 |
|
|
десятичная |
|
0,1,2,3,4,5,6,7,8,9 |
|
|
8 |
0,1,2,3,4,5,6,7 |
|
|
2 |
|
2.18. Заполните следующую таблицу:
|
Система счисления |
Основание |
Разряды (степени) | ||||
|
десятичная |
10 |
10000 |
1000 |
100 |
10 |
1 |
|
восьмеричная |
8 |
|
|
|
|
|
|
двоичная |
2 |
|
|
|
|
|
2.19. Запишите в развернутом виде числа:
|
а) А8=143511; |
г) А10=143,511; |
|
б) А2=100111; в) А16=143511; |
д) А8=0,143511; е) А16=1A3,5C1. |
2.20. Запишите в свернутой форме следующие числа:
|
а) А10= 9·101+1·100+5·10-1+3·10-2; |
|
б) А16=А·161+1·160+7·16-1+5·16-2. |
2.21. Правильно ли записаны числа в соответствующих системах счисления:
|
а) А10=А,234; б) А8=-5678; |
в) А16=456,46; г) А2=22,2; |
2.22. Какое минимальное основание имеет система счисления, если в ней записаны числа 127, 222, 111? Определите десятичный эквивалент данных чисел в найденной системе счисления.
2.23. Чему равен десятичный эквивалент чисел 101012, 101018 1010116?
2.24. Трехзначное десятичное число оканчивается цифрой 3. Если эту цифру переместить на два разряда влево, т.е. с нее будет начинаться запись нового числа, то это новое число будет на единицу больше утроенного исходного числа. Найдите исходное число.
2.25. Шестизначное десятичное число начинается слева цифрой 1. Если эту цифру перенести с первого места слева на последнее место справа, то значение образованного числа будет втрое больше исходного. Найдите исходное число.
2.26. Какое из чисел 1100112, 1114, 358 и 1В16 является:
а) наибольшим;
б) наименьшим.
2.27. Существует ли треугольник, длины сторон которого выражаются числами 128, 1116 и 110112?
2.28. Какое наибольшее десятичное число можно записать тремя цифрами в двоичной, восьмеричной и шестнадцатеричной системах счисления?
2.29. «Несерьезные» вопросы.
Когда 2x2=100 ?
Когда 6x6=44?
Когда 4x4=20?
2.30. Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам:
|
а) [1011012; 1100002]; б) [148; 208]; |
в) [2816; 3016].
|
2.31. В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе?
2.32. В классе 36q учеников, из них 21q девочек и 15q мальчиков. В какой системе счисления велся счет учеников?
2.33. В саду 100q фруктовых деревьев, из них 33q яблони, 22q груши, 16q слив и 5q вишен. В какой системе счисления посчитаны деревья?
2.34. Было 100q яблока. После того как каждое из них разрезали пополам, стало 1000q половинок. В системе счисления с каким основанием вели счет?
2.35. У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?
2.36. Некогда был пруд, в центре которого рос один лист водяной лилии. Каждый день число таких листьев удваивалось, и на десятый день вся поверхность пруда уже была заполнена листьями лилий. Сколько дней понадобилось, чтобы заполнить листьями половину пруда? Сколько листьев было после девятого дня?.
2.37. Путем подбора степеней числа 2, в сумме дающих заданное число, переведите в двоичную систему счисления следующие числа:
|
а) 5; б) 7; в) 12; |
г) 25; д) 32; е) 33. |
Проверить правильность перевода с помощью программы Advanced Converter.
Сайт сделан по технологии "Конструктор школьных сайтов".